Unique Info About Why We Use Mle Instead Of Ols Interpreting Line Plots Answer Key

Ordinary least squares is a method used to estimate the coefficients in a linear regression model by minimizing the sum of the squared residuals.

Why we use mle instead of ols. Mle runs a bunch of trials and finds a lline (but not in the same sense as ols). Using the logistic loss function causes large errors to be penalized to an asymptotic constant. We use ordinary least squares (ols), not mle, to fit the linear regression model and estimate b0 and b1.

To use ols method, we apply the below formula to find the equation. Ols for estimating ar (p) so i've been reading that ols is biased with ar (p) models (though i'm confused because it seems like people estimate it with ols.

If the model predicts the outcome is. Is it to compare with other regression models with the same response and a different predictor?. Ols draws a flat line (this is where the term linear comes from, ofcourse) through a set of data.

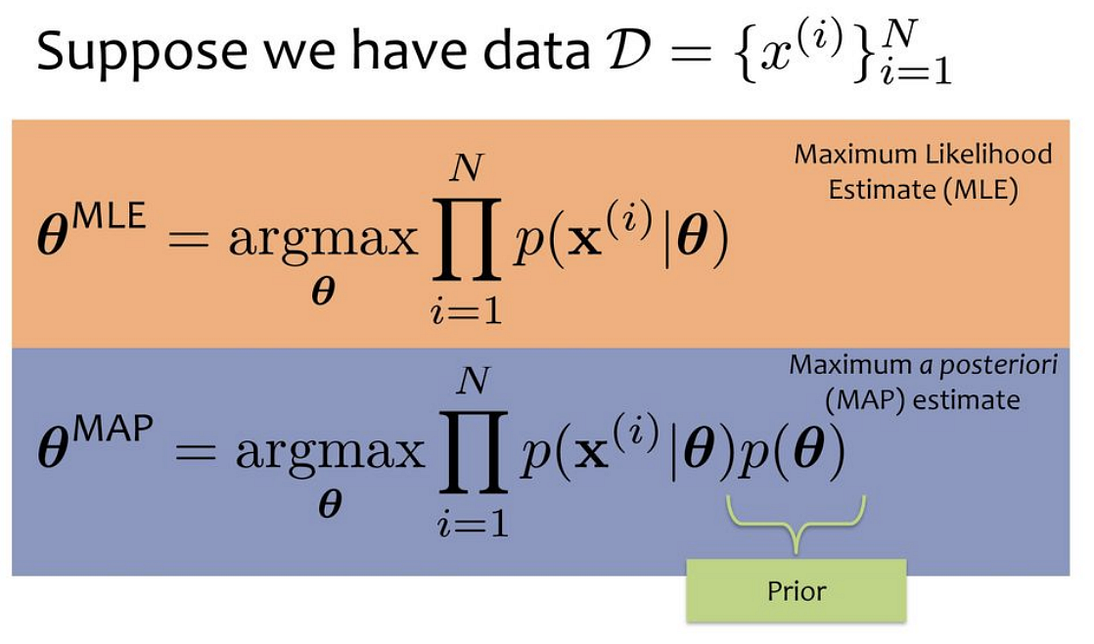
In the case of normally distributed data, ols converges with the mle, a solution which is blue (in that point). We can extract the values of these parameters using maximum likelihood estimation (mle). In order to understand the similarities or dissimilarities between ols & mle, we need to carefully understand the definition the two commonly interchangeable words.

However, depending on the data and what exactly. Consider linear regression on a categorical {0,1} outcomes to see why this is a problem. Once out of normal, ols isn't blue anymore (in the terms of.

This is where the parameters are found that maximise the likelihood. We introduced the method of maximum likelihood for simple linear regression in the notes for two lectures ago. We start with the statistical model, which is the.

It turns out that for a linear model, the model coefficients estimated by ols are identical to those estimated using mle because maximizing the likelihood is. Ols (ordinary least squares) and mle (maximum likelihood estimation) are statistical methods used in regression analysis, but ols estimates regression. This tutorial is to compare ols (ordinary least square) and maximum likelihood estimate (mle) in linear regression.

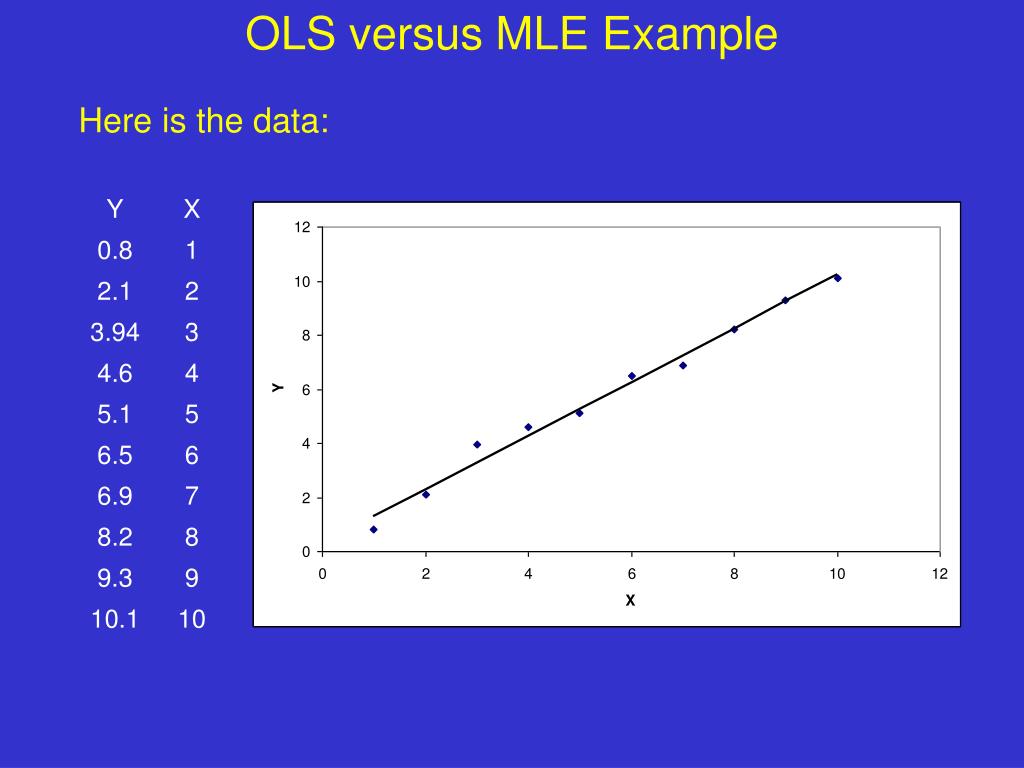
We will use ordinary least squares method to find the best line intercept (b) slope (m) ordinary least squares (ols) method. We are going to use simple linear. We need to calculate slope ‘m’ and line intercept ‘b’.

What's the use of knowing the value of the likelihood function? This tutorial shows how to estimate linear regression in r using maximum likelihood estimation (mle) via the functions of optim() and mle().