Can’t-Miss Takeaways Of Info About Is Heap Faster Than Sorting Different Types Of Line Charts

The bigger issue than the potential for fraud or maladministration is that the voters have lost confidence in the system, heap said.

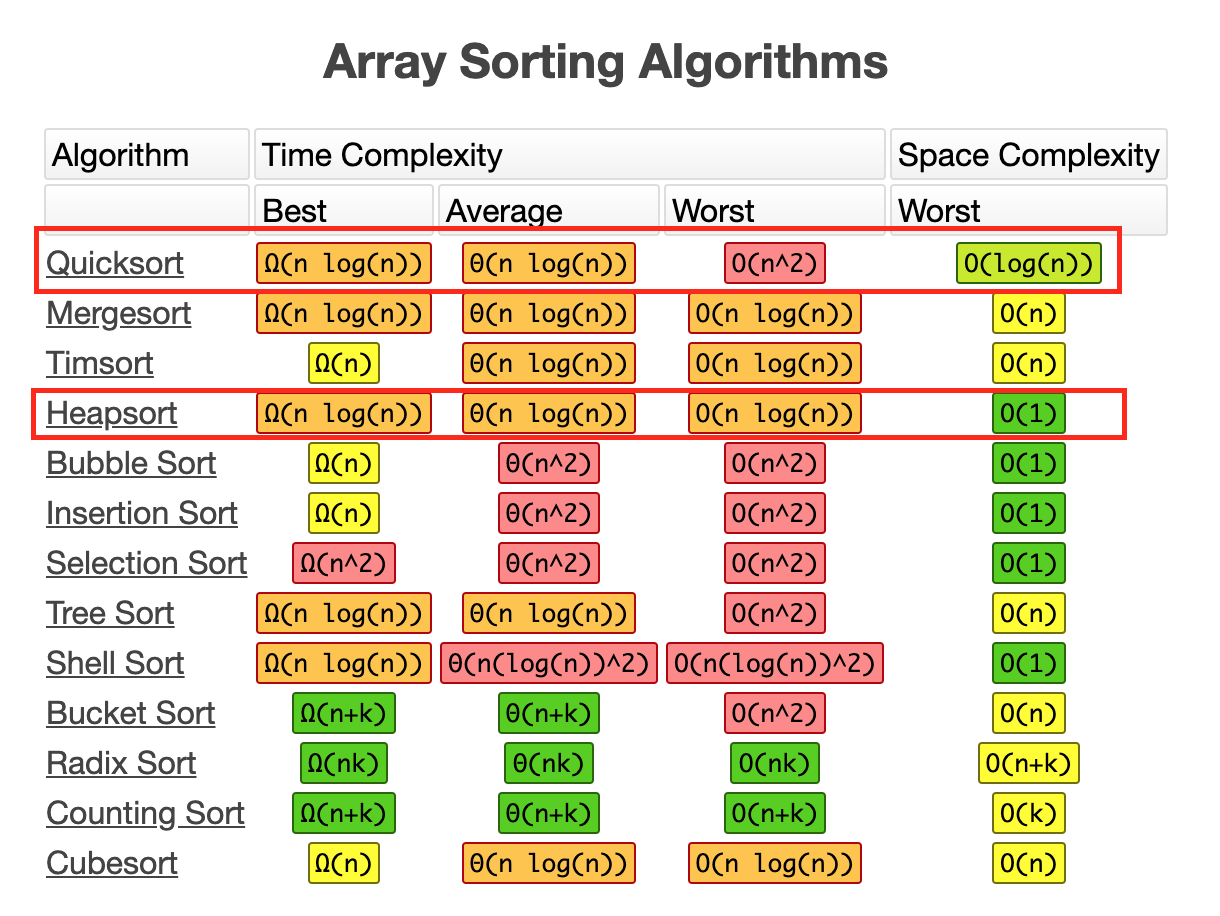
Is heap faster than sorting. Heap sort is a safe bet when dealing with very large inputs. Heap sort takes space. Additions and insertions could come in unspecified order.

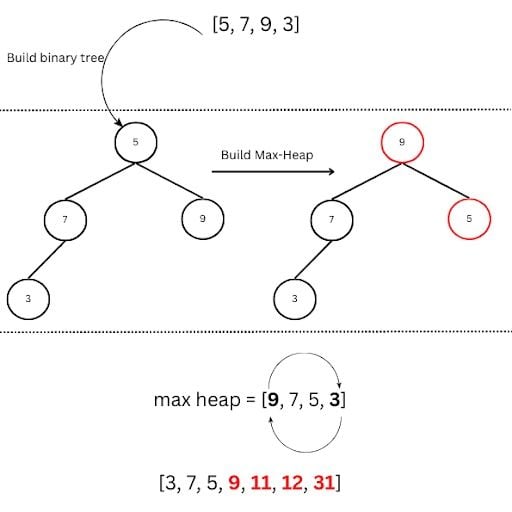
As my answer over there said, timsort is generally better than quicksort: The heapq is faster than sorted in case if you need to add elements on the fly i.e. The paper also introduced the binary heap as a useful data.

At the first glance, things are clear: Two heaps for the smallest and largest element are still a lot faster (but that situation is quite rare; Quicksort executed almost 4.6 times less.

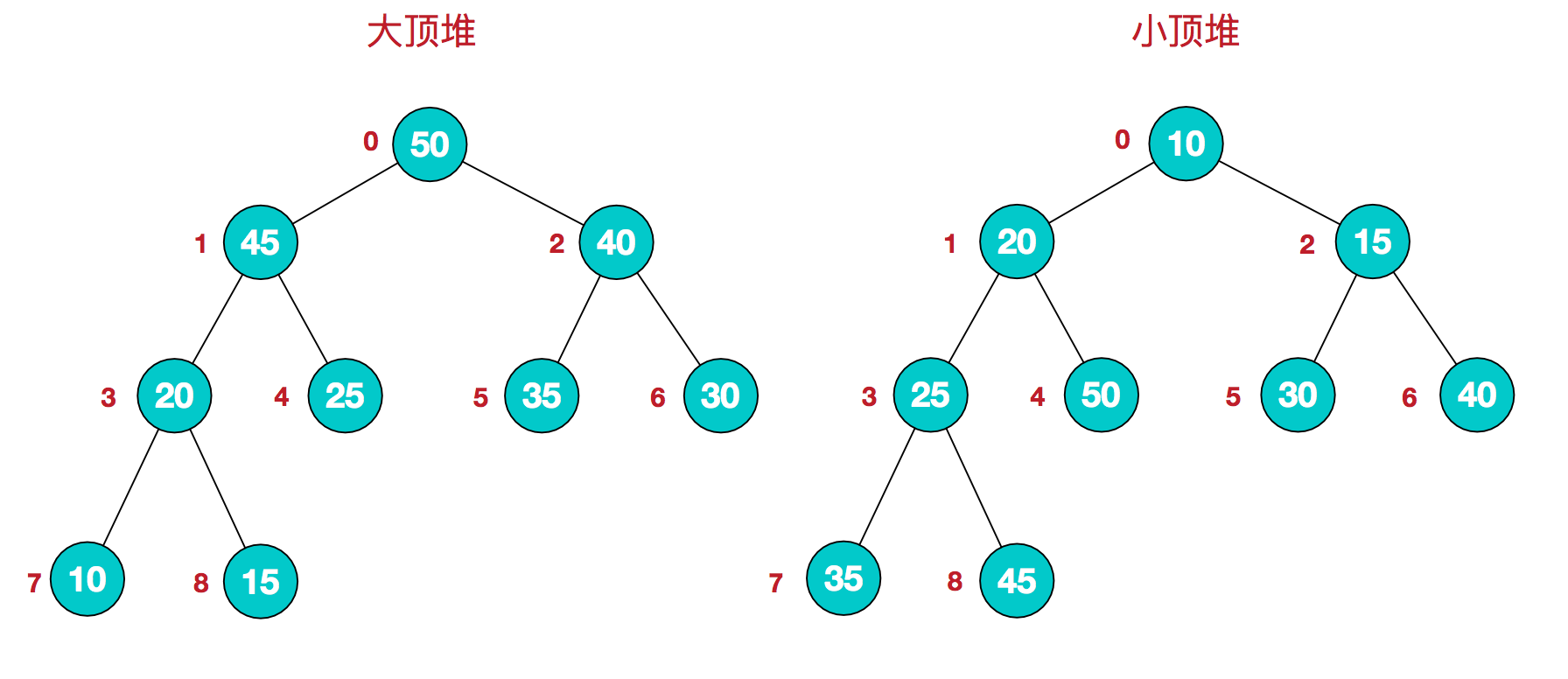
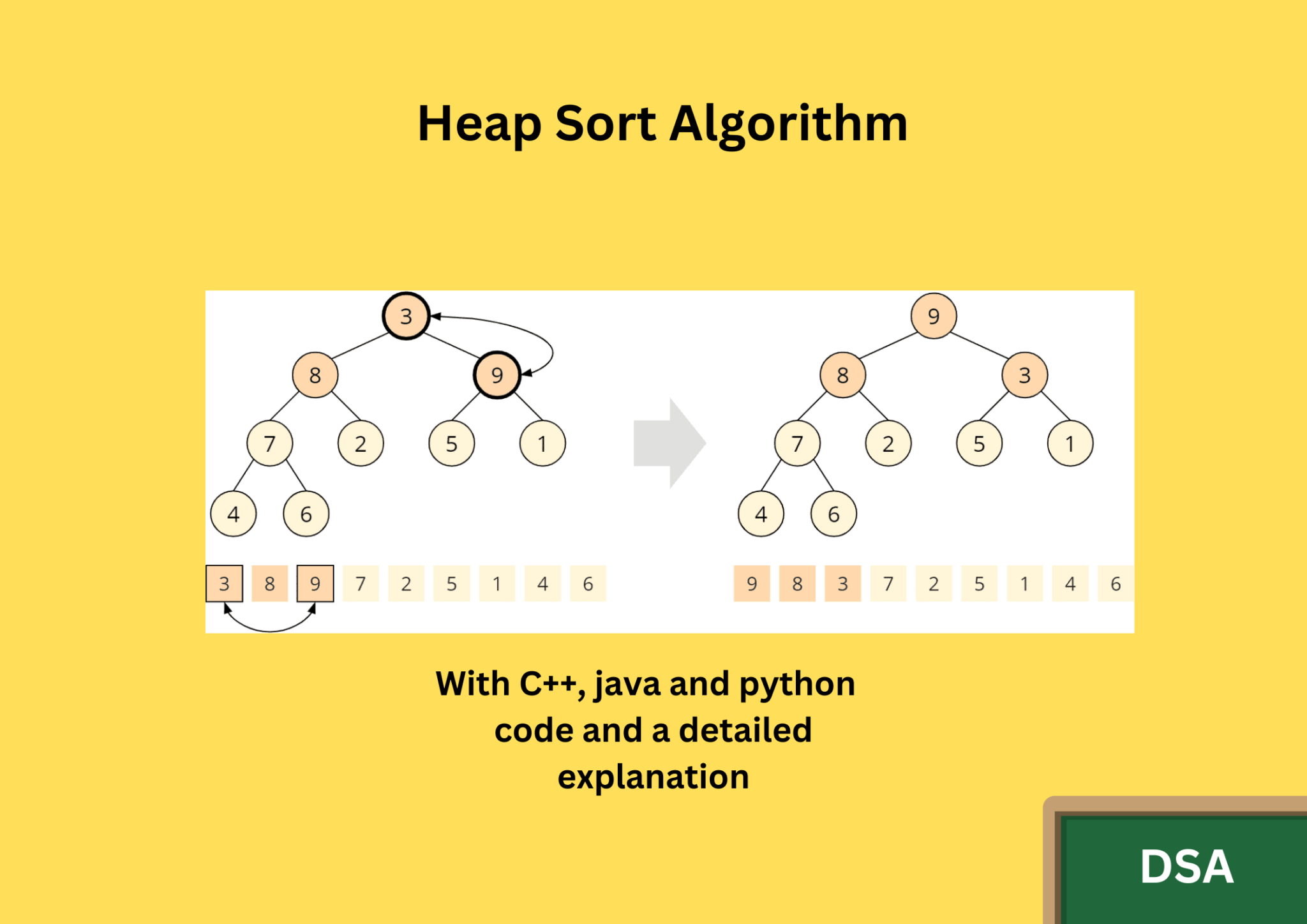
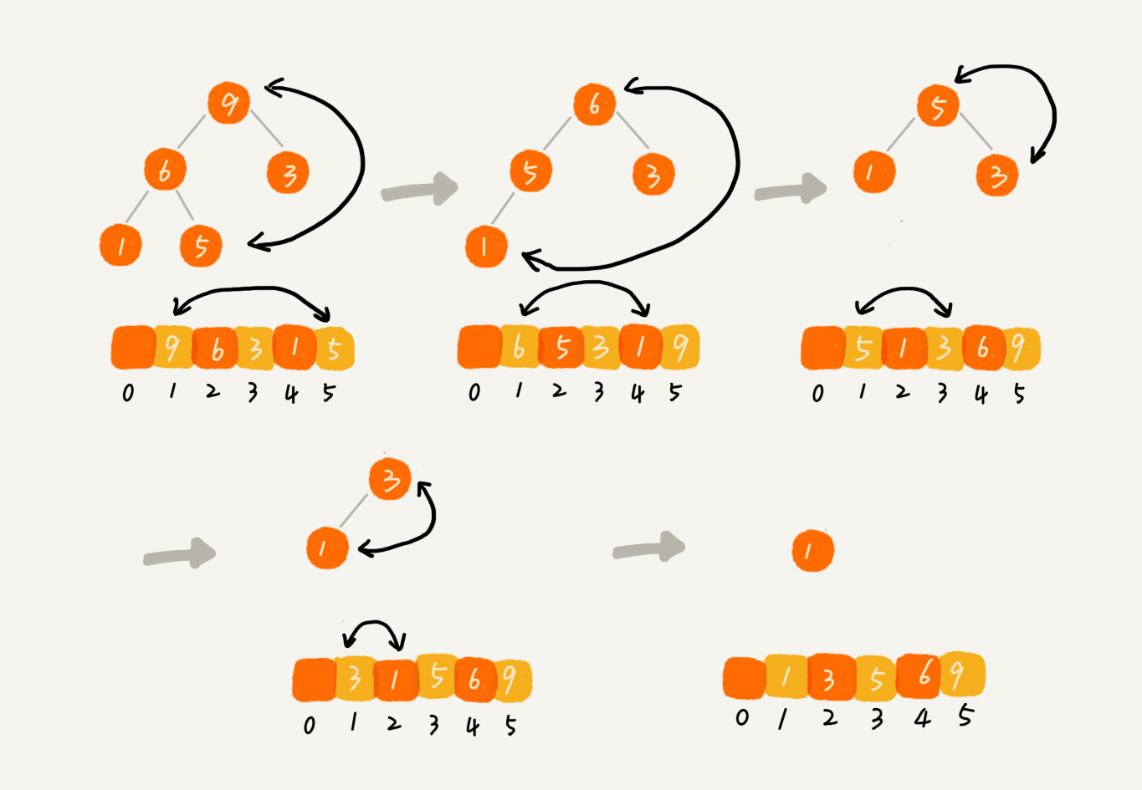
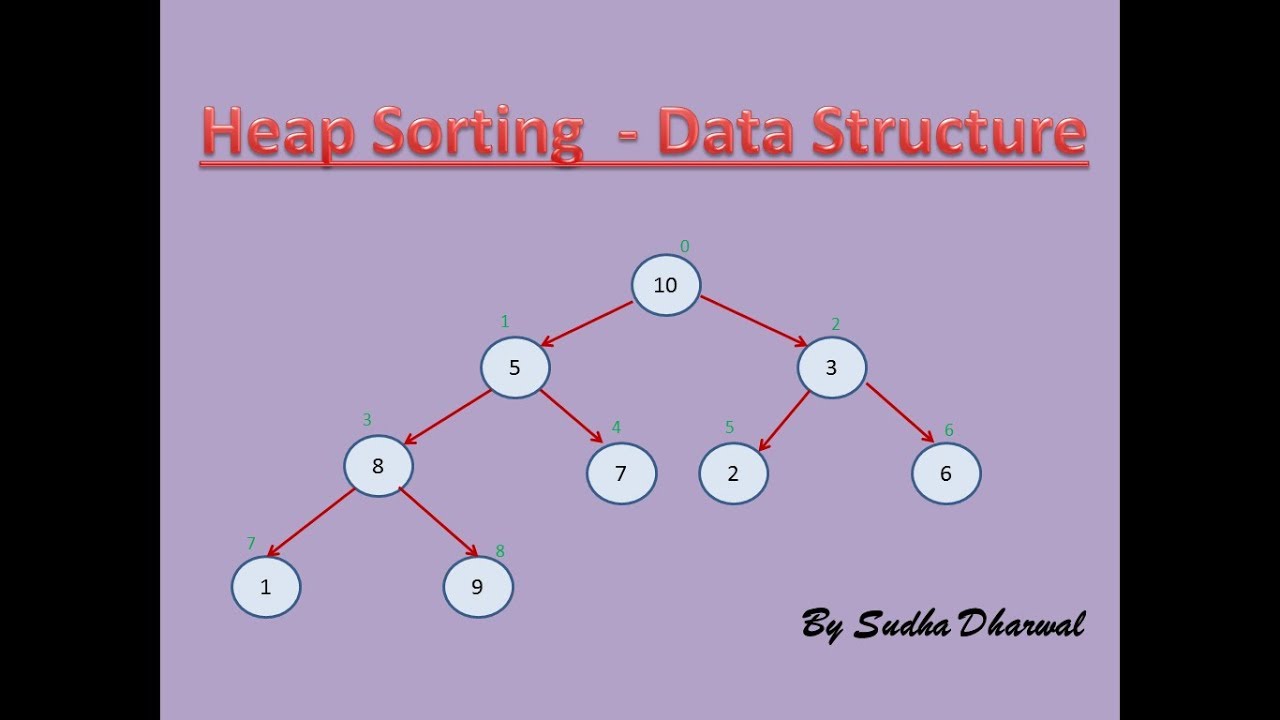
You can see the best, average and worst time complexity of heap sort are all o (n logn) but it’s o (n^2) for worst of quick sort. The complete binary tree is balanced, its array representation is space efficient,. Heapsort is about 3 times slower than quicksort, and the reason is simple:

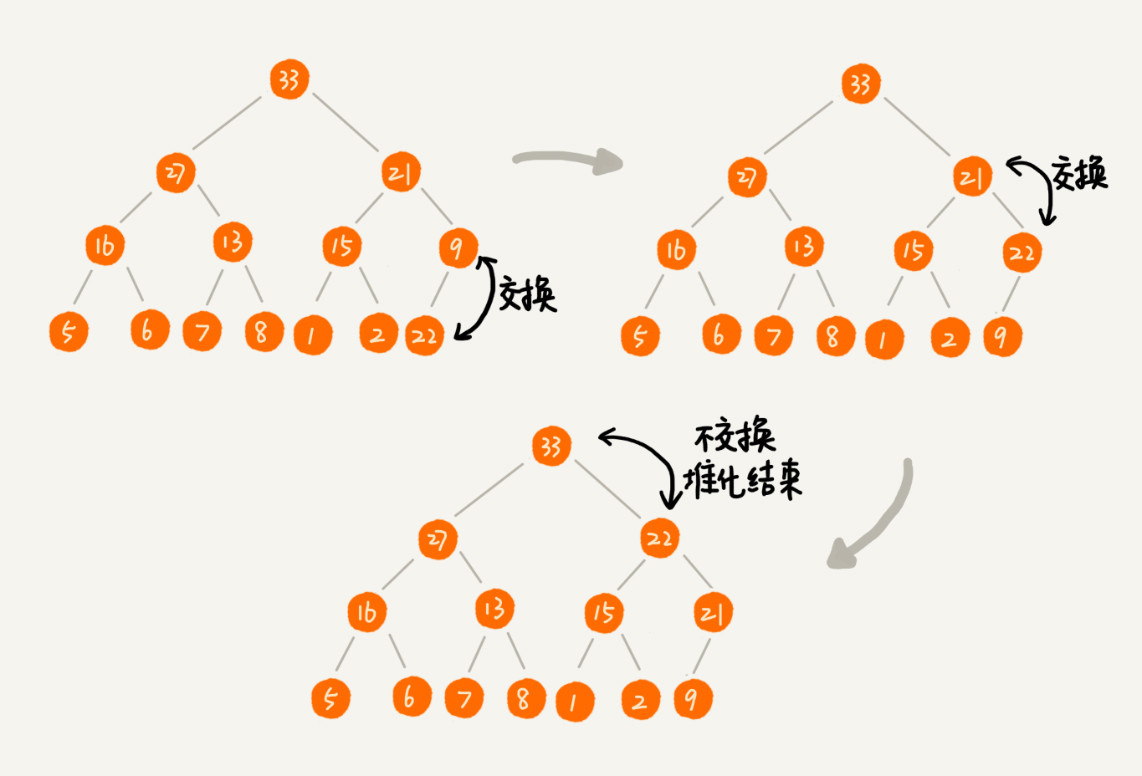
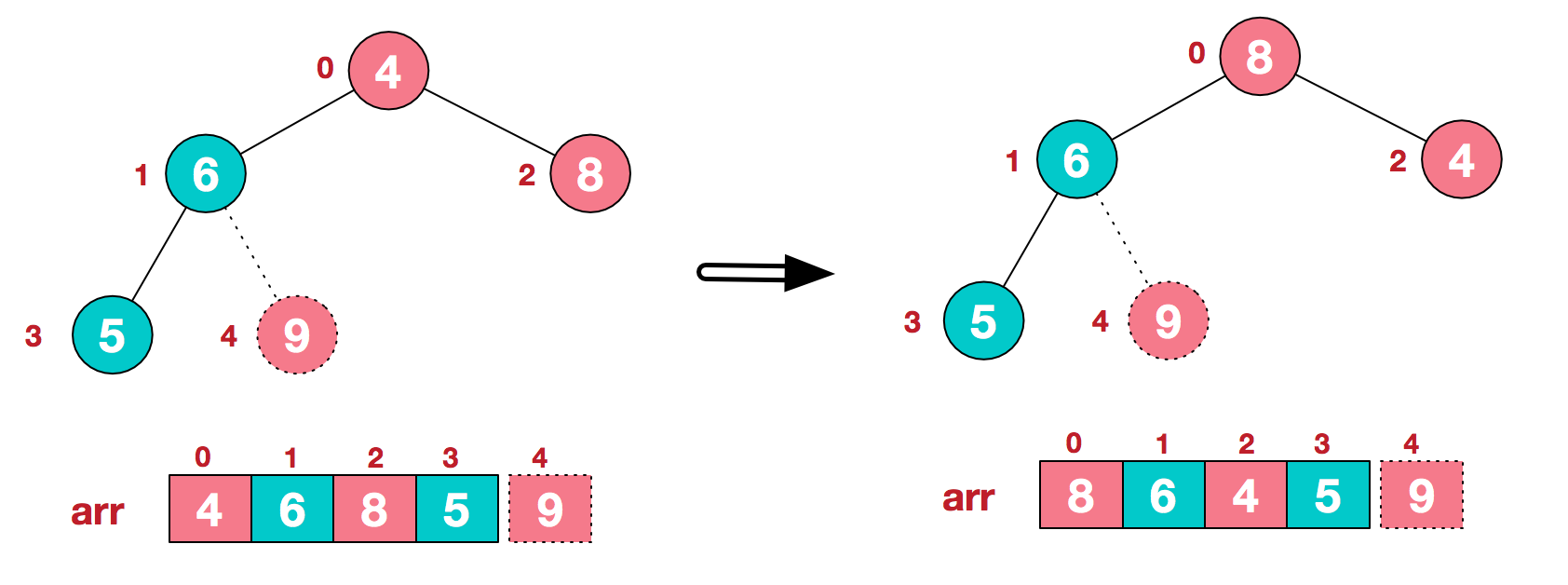
Swap the smallest element (at index 0) with the last element in the heap, bubble that element down until the heap property is. For example, for the array of size 1000000, heap sort took 3.68. While it has a time.

I found that the heap sort code performs exceptionally better in all cases as compared to merge sort. Then why do we always use quick. Heapsort was invented by j.

Using a heap to find the smallest element is definitely a lot faster than sorting an array. While the asymptotic complexity of heap sort makes it look faster than. While heap sort removes recursive calls by tail optimization and its space requirement is $o(1)$, quick sort requires variables put on the stacks at each recursive.

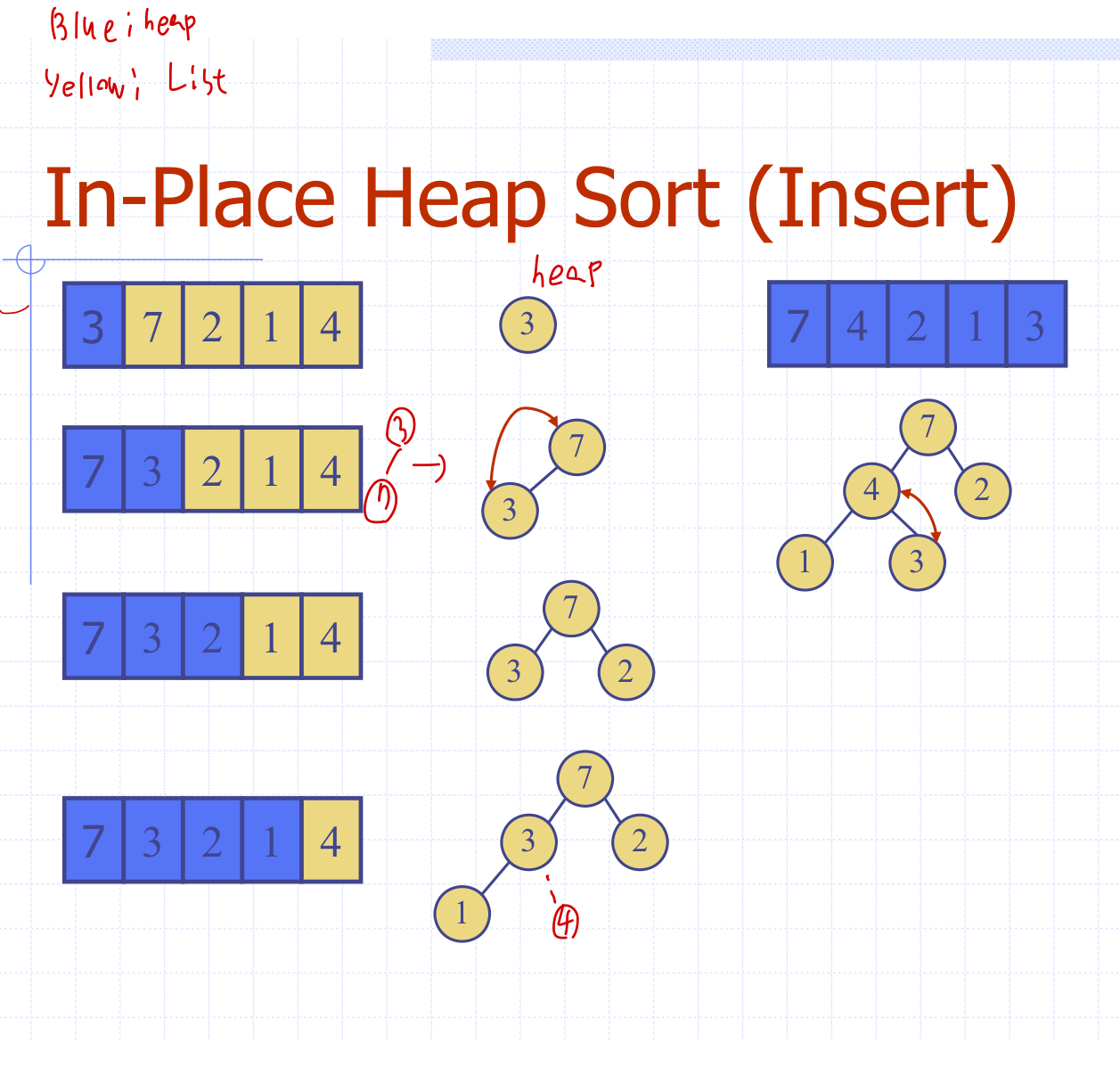
Stable (unlike quicksort), same asymptotic speed as quicksort for random data (and roughly same. Heapsort has all of the advantages just listed. I thought, since you can build a heap in o(n) it must be faster to pop 25 elements (each being o(logn)) than sorting the whole vector in o(nlogn).

That's way better than merge sort's overhead. I am doing a performance test on different sorting methods, and the heapsort code from geeksforgeeks is slower than the selection sort. The answer lies in the comparison of their time complexity and space requirements.