Wonderful Tips About Closed Dot On Number Line Node Red Chart Multiple Lines

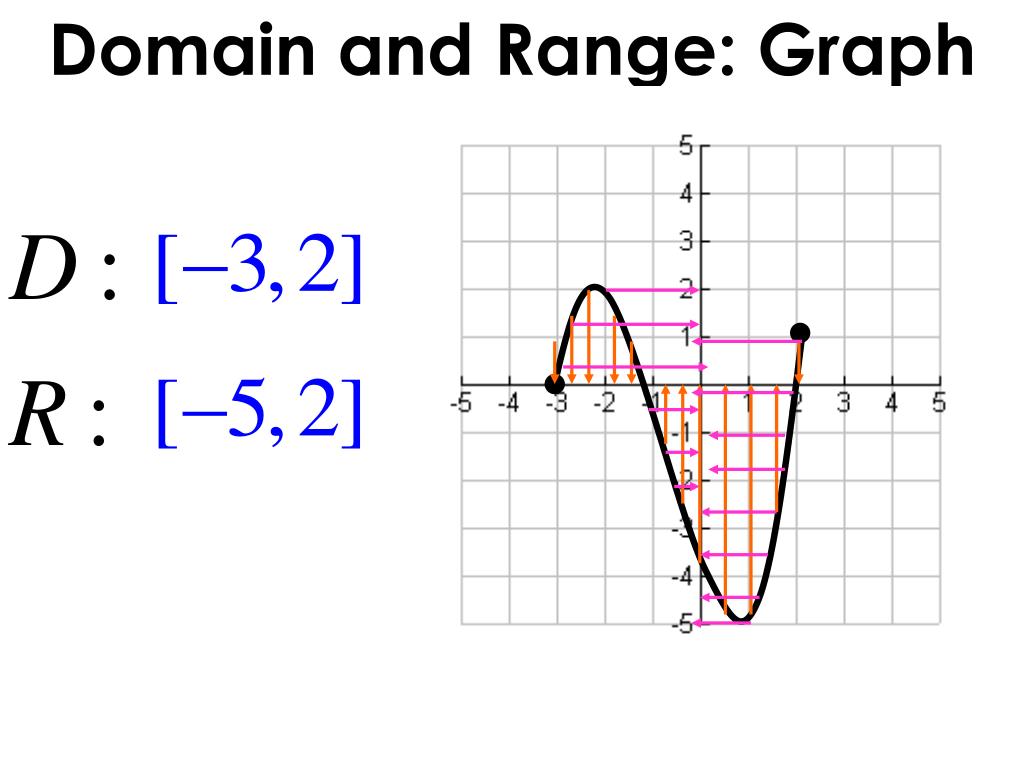
Take a look at the given graph on the number line and identify these two things on the graph:

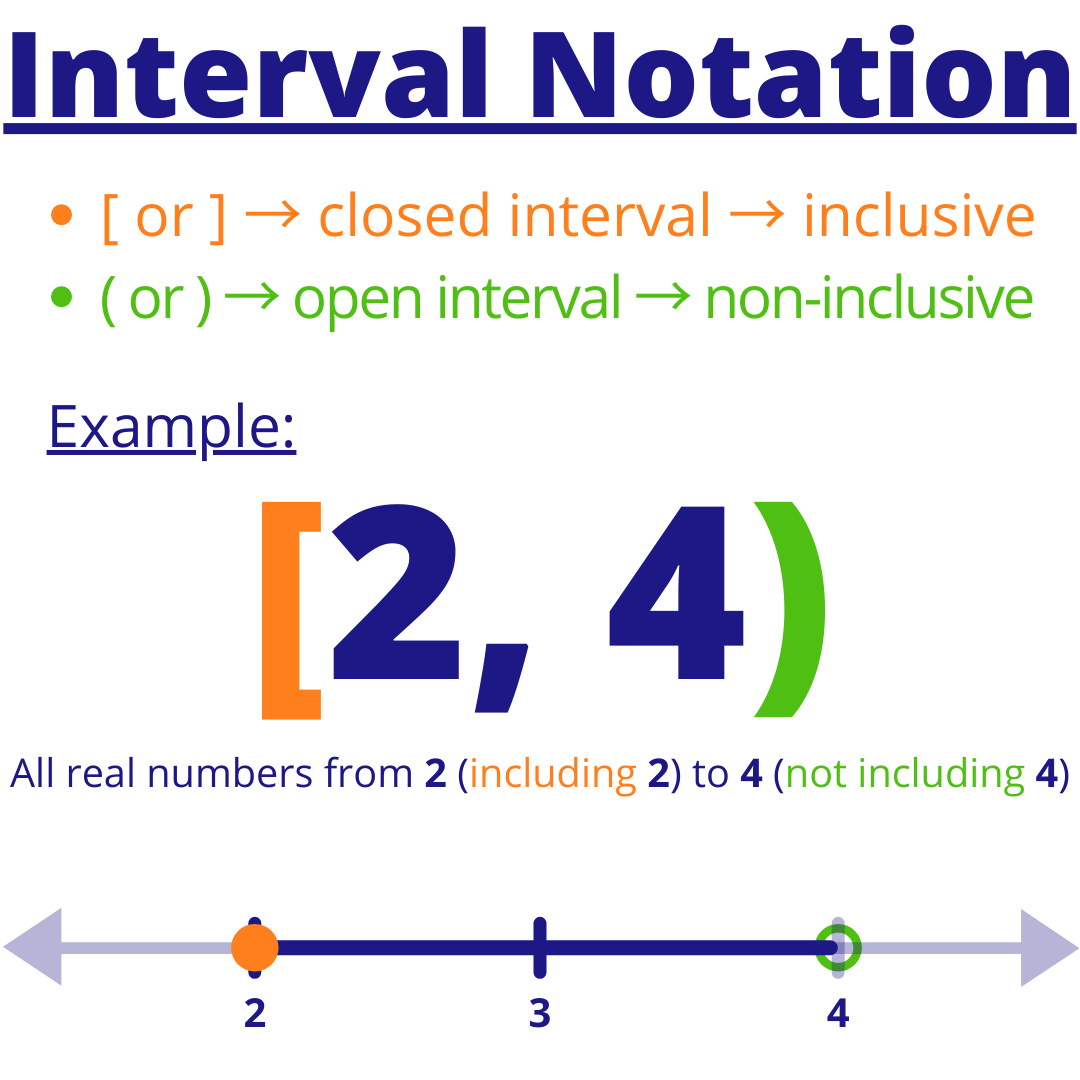
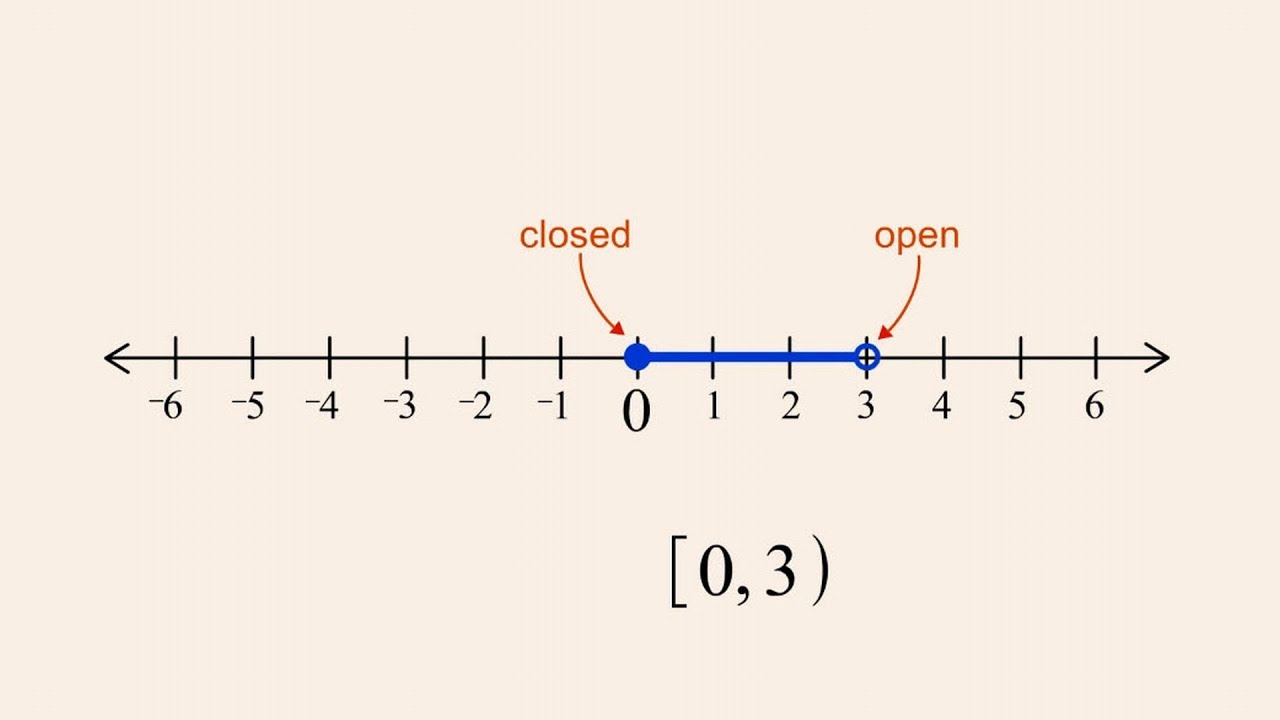
Closed dot on number line. A closed dot on a number line means that the number at that point is included in the set or range. 1) draw a number line. For ≤ and ≥ , use a closed dot to.

The line continues to the. Graph the solution of x ≥ 0 on a number line. So a closed dot means the point counts and you need the equal sign below the line (≥ or ≤).

Example 1 graph the set of x such that 1 ≤ x ≤ 4 and x is an integer (see figure 2). Graph of the point 2. For example, notice that for the graph of x≥ −3 x ≥ − 3 shown above, the end point is −3 − 3, represented with a closed circle since the inequality is greater than or equal to −3 − 3.

X <9 x < 9 indicates the list of numbers that are less than 9 9. Draw an arrow going from the closed dot, along the number line to the left and explain that the solution includes 12 and all of the numbers less than 12. 2) put either an open circle or a closed dot above the number given.

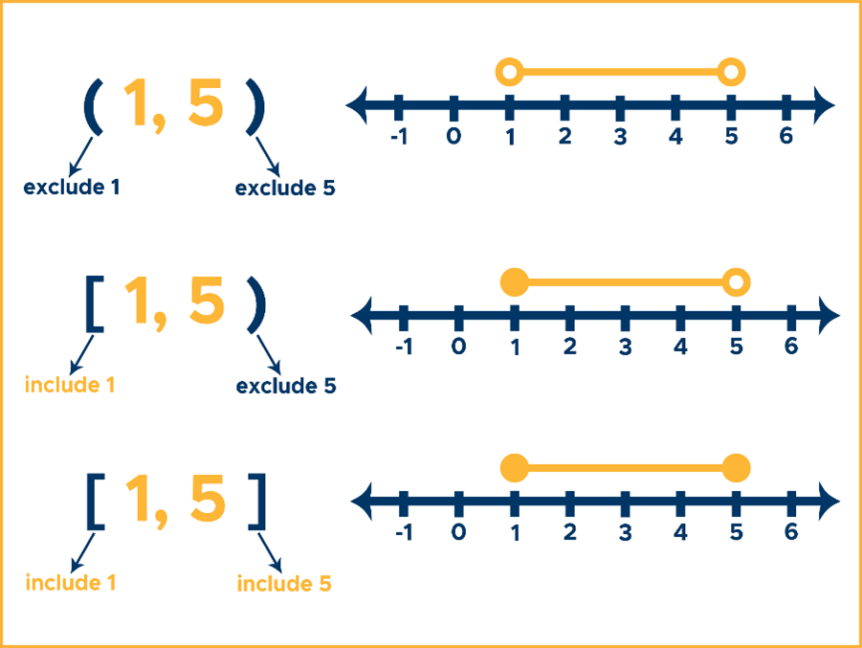
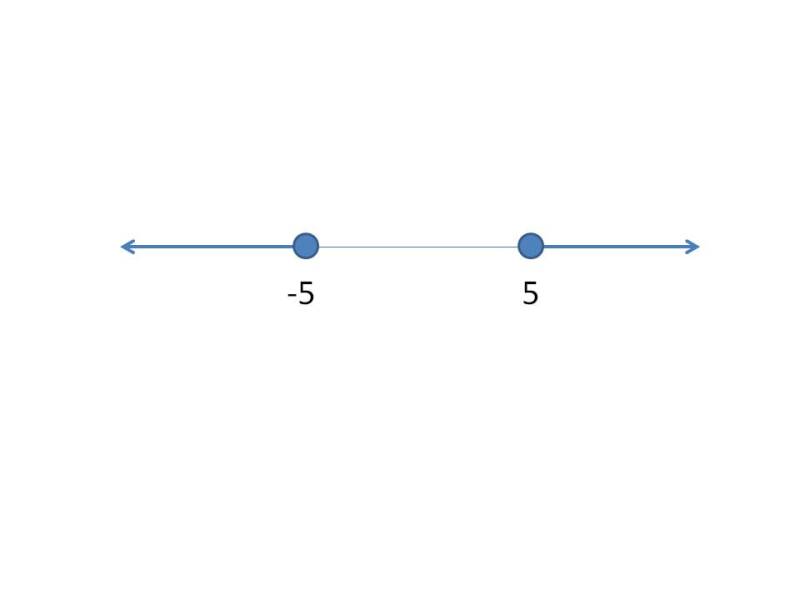
Because of the strict inequality, plot them using open dots on a number line. Closed circles are used for numbers that are less than or equal to and greater than or equal to (≤ or ≥). A graph of {x:1 ≤ x ≤ 4, x is an integer}.

When graphing the solutions of an inequality, what is the difference between an open dot and a closed dot? This will depend on whether the endpoint is included in the range of values (we will go into more detail on. Hi cynthia, suppose that you.

An open circle on a number line expresses that the. Here the critical values are: For example, this is the number line for the inequality \(x \geq 0\):

The direction to which the arrow is pointing an open or closed dot at the start. { x :1 ≤ x ≤ 4, x is an integer} figure 2. The line shows all of the.

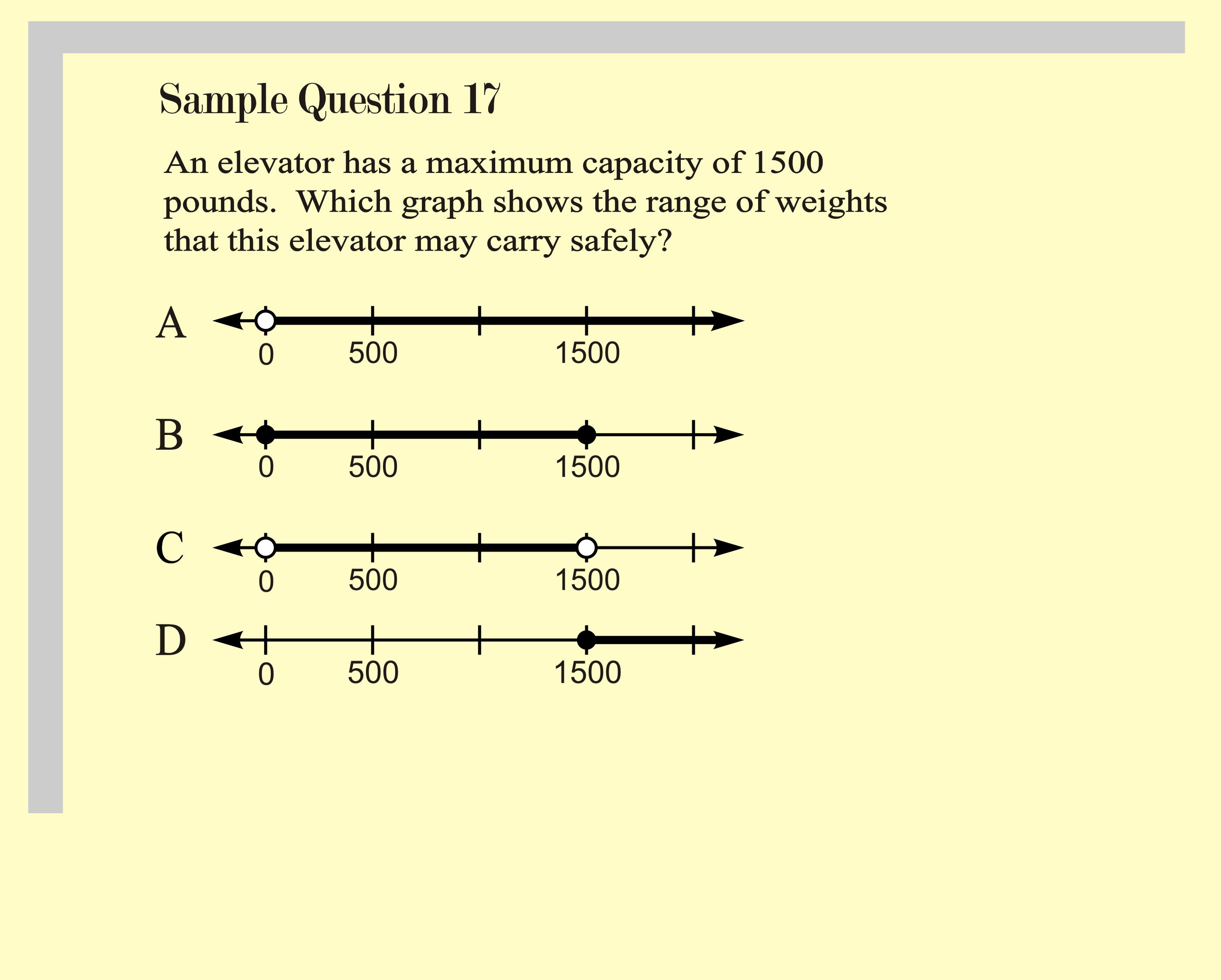
Here is a summary of how to graph inequalities: Let's practice using a number line: To graph this inequality, you draw a closed circle at the end point 16 on the number line to show that solutions include the value 16.

Applications the “greater than or equal to” (≥) relation, especially when visualized on. Closed circles are used for numbers that are less than or equal to and greater than or equal to (≤ or ≥). The symbol (∞) is read as infinity and indicates that the set is unbounded to the right on.