Neat Tips About How Many Edges Can A Graph Have To Make Statistics In Excel

Polling averages help us incorporate polls that point in different directions and let us easily compare trends.

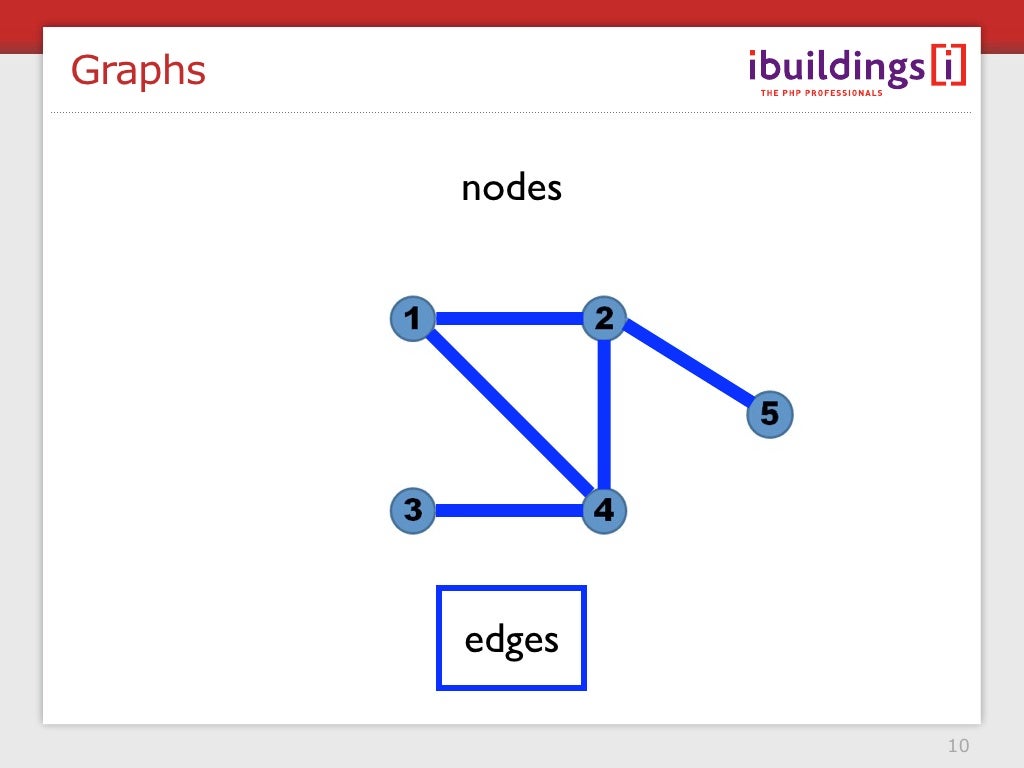
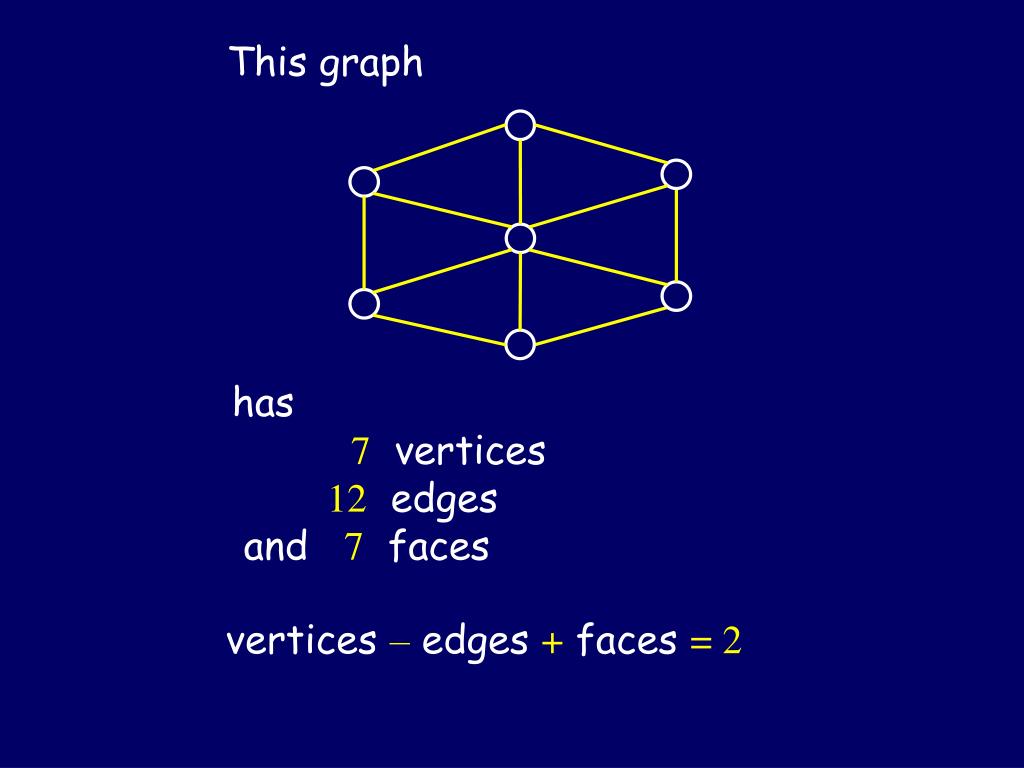
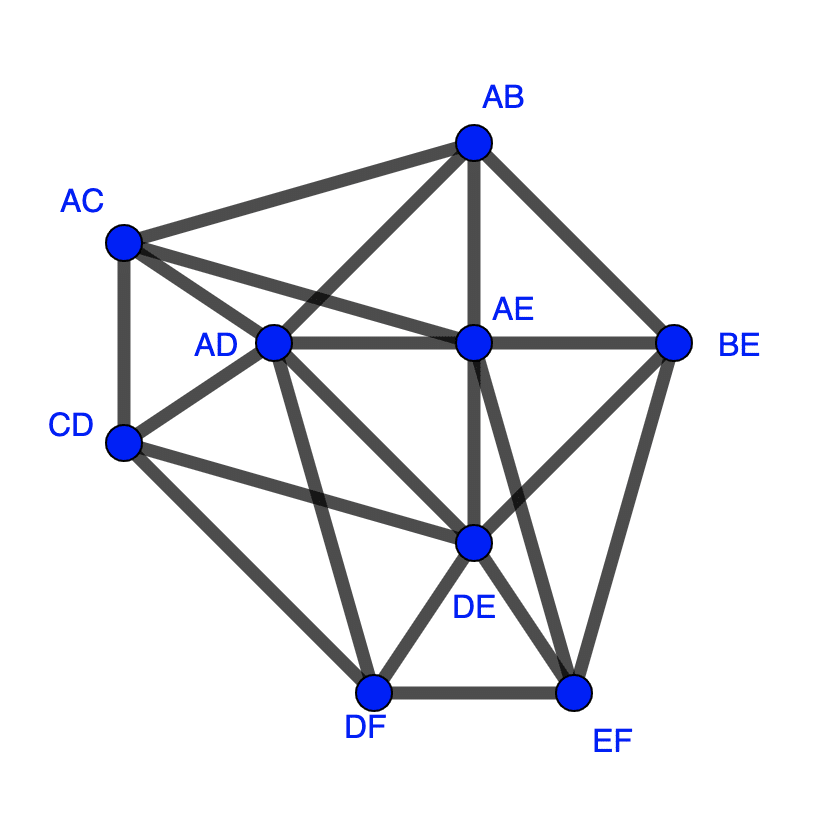
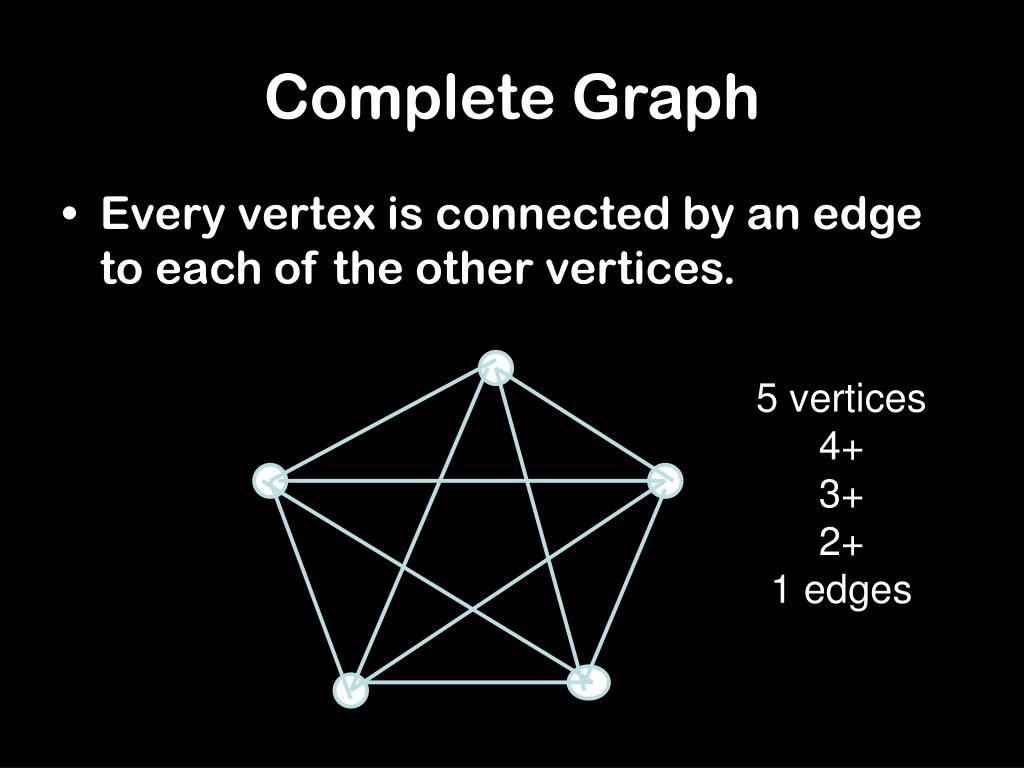
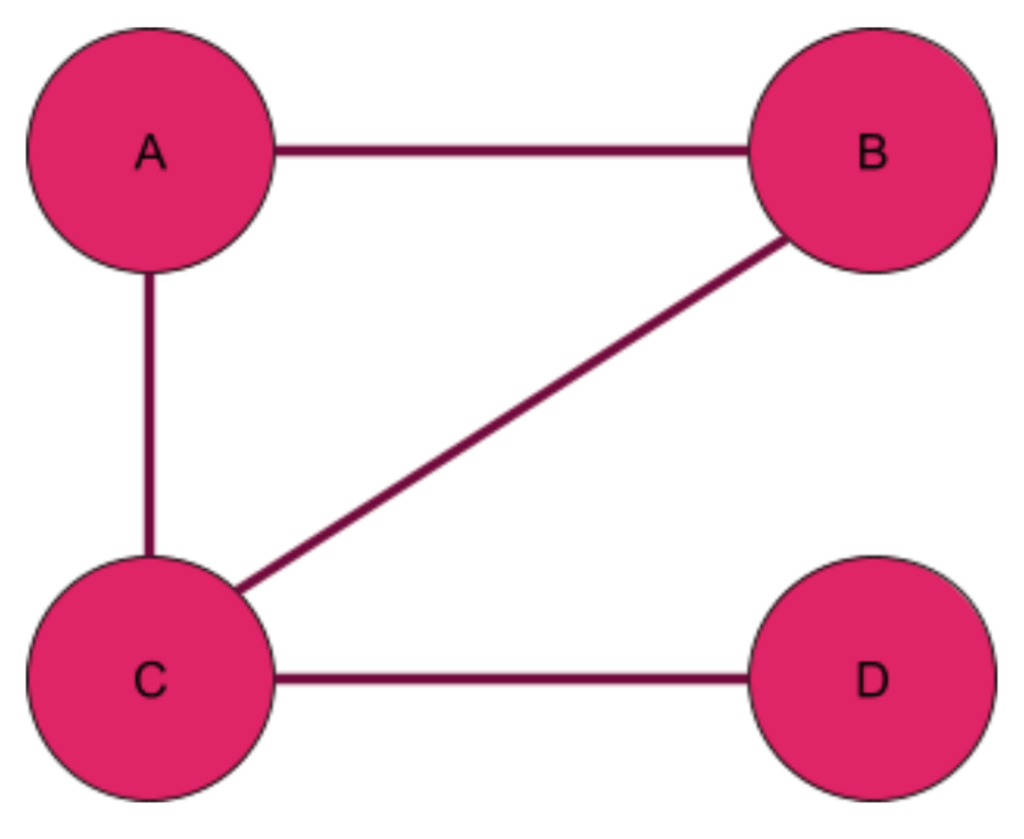
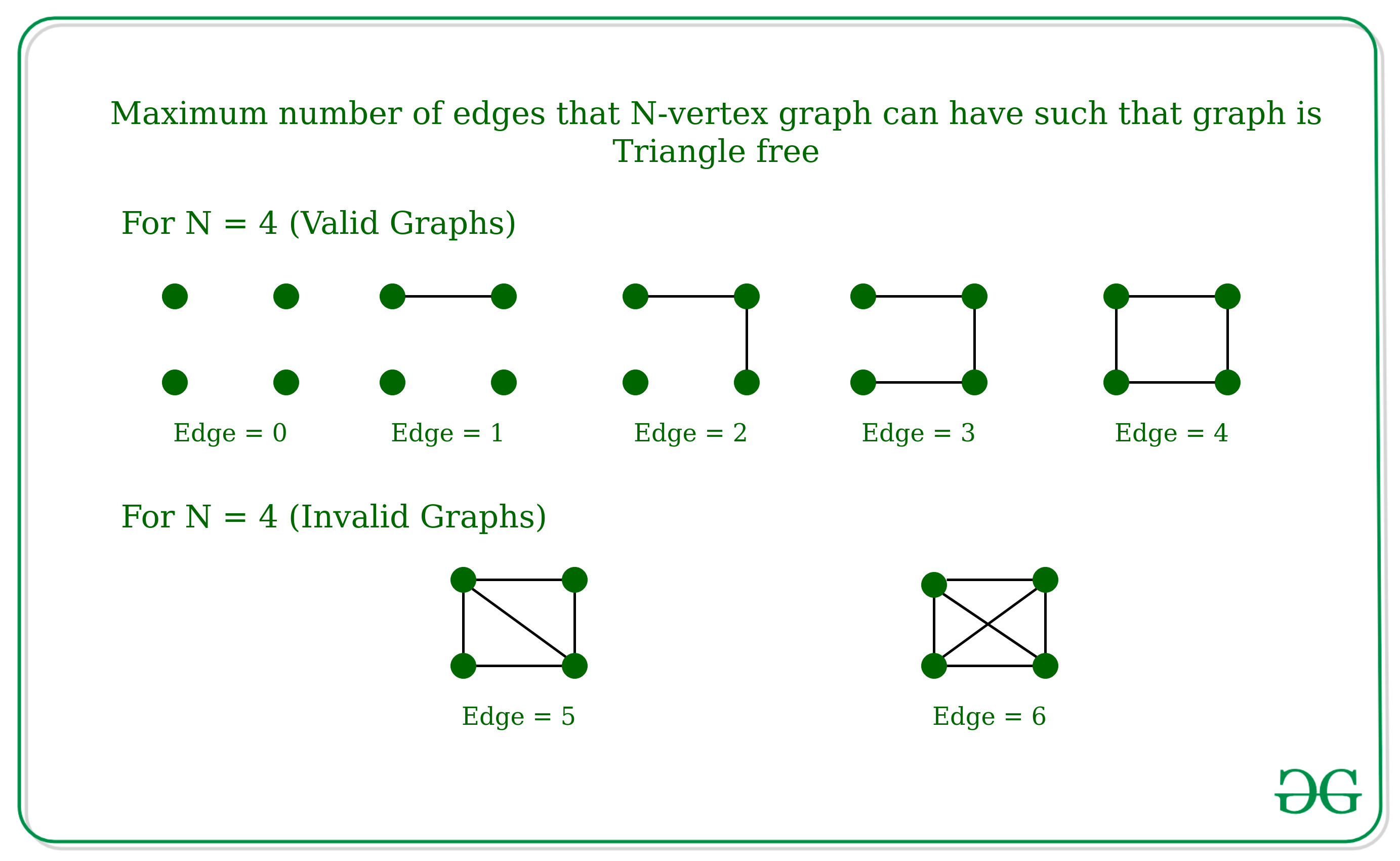
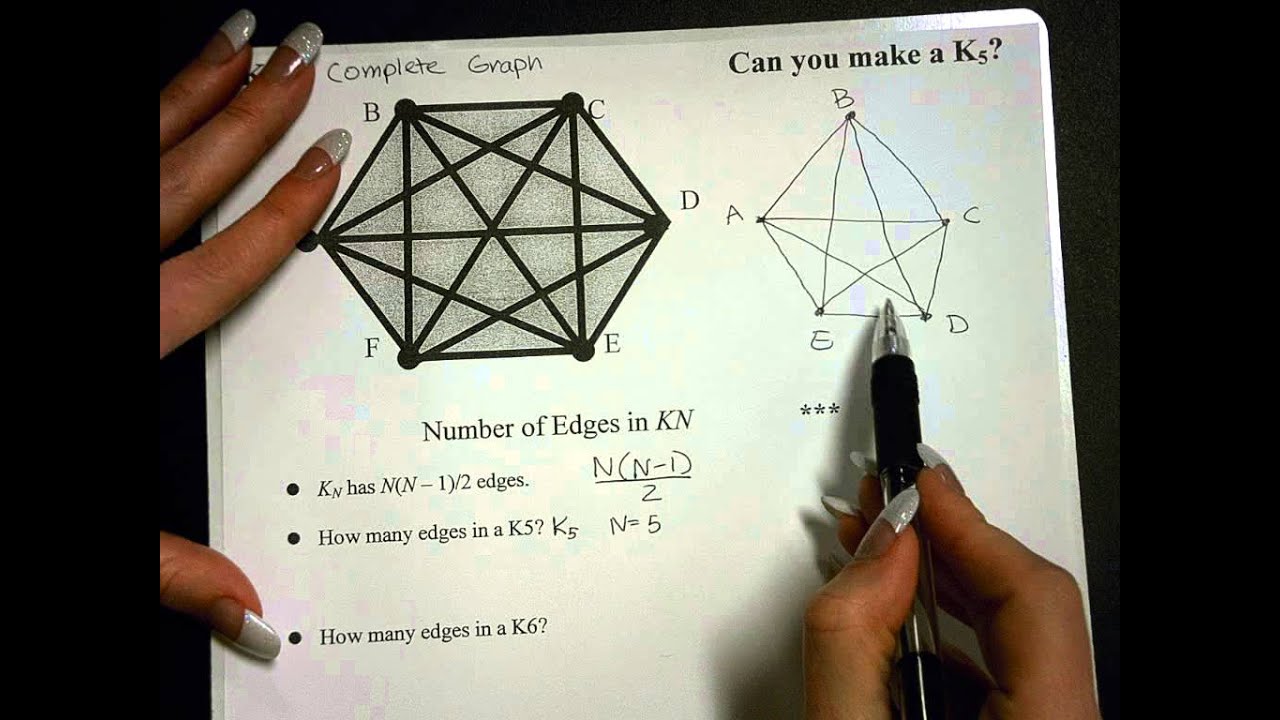
How many edges can a graph have. I'm doing a question in my text that asks me to find how many regions a graph has if it has 6 vertices all of which has degree 4. For that, consider n points (nodes) and ask how many edges can one make from the first point. Look over k_n (the complete graph with n vertices) which has the maximum number of edges.

Edges = m * n where m and n are the number of edges in both the sets. In chemical structures, each atom can be defined as a node and each bond as an edge, which can be analyzed for biological activity for new drug discovery. We demonstrate that metaspots can be used to reduce the size of.

In order to maximize the number of edges, m must be equal to or as close to n as possible. The maximum number of edges in a dag with n vertices is $\theta(n^2)$. Continue for remaining nodes, each.

A complete graph means that every vertex is connected with every other vertex. The number of edges will be maximum when every vertex of a given set has an edge to every other vertex of the other set i.e. The maximum number of edges in the directed graph depends on the number of the vertices and type of graph.

Since it is a simple graph, we cannot have any parallel edges. Even if the vertex at each end of the edge is the same vertex, it's still counted twice.

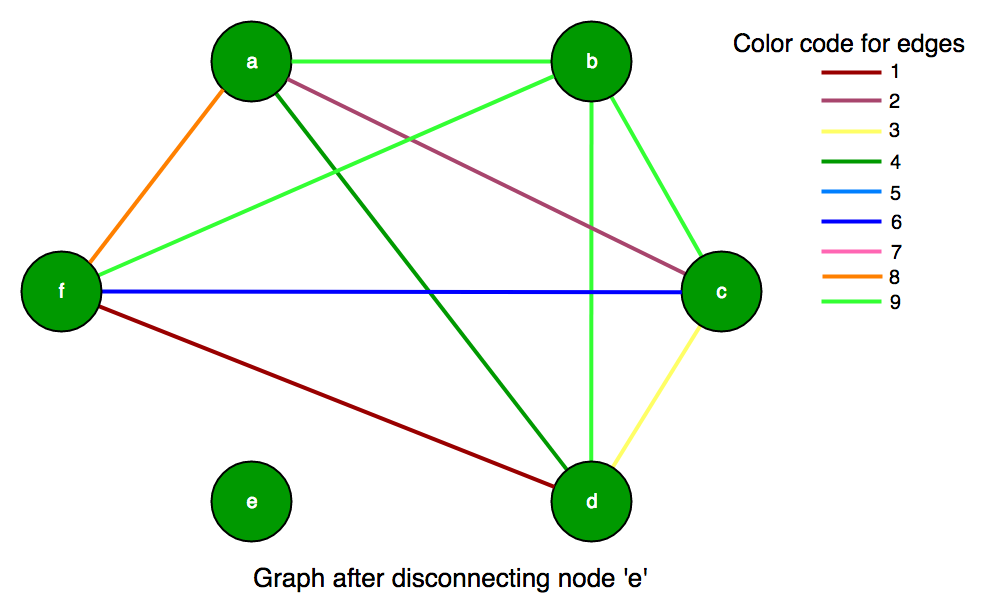
So any edge we add will then join the two components together and ensure that g is connected. Graph data types mainly consist of nodes and edges. What is the maximum number of edges that the graph g can have?

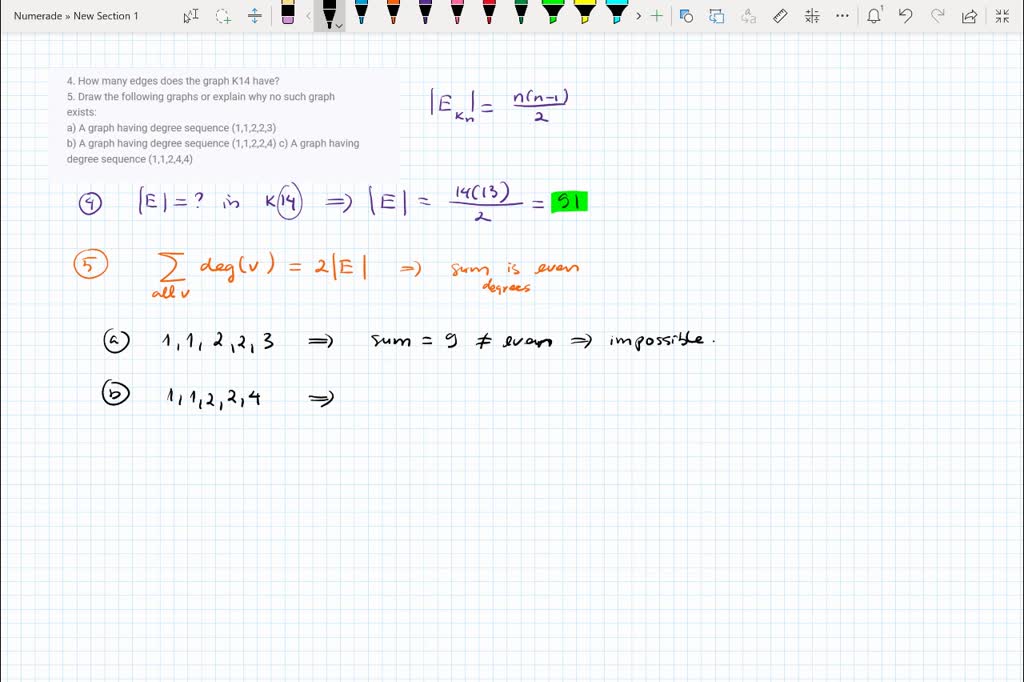
Where n = n = number of vertices. Consequently, graph convolutional networks (gcns) have been proposed for such datasets. Since e is subet or equal to v x v, graph g contains at most v^2 edges.

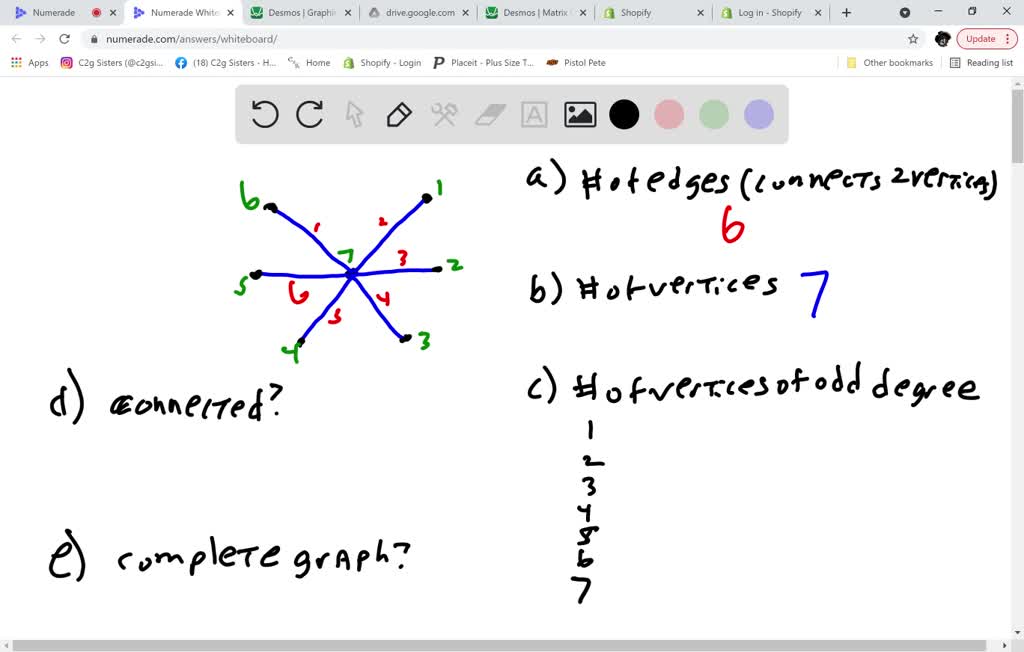
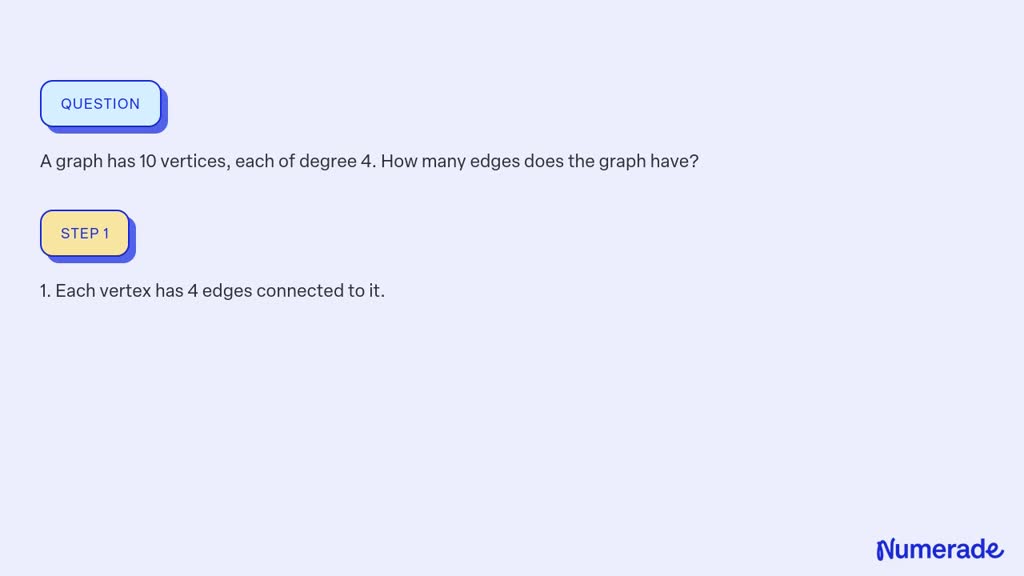
I now, the handshaking theorem tells us that. Therefore, the main concern when designing a graph representation scheme is to find a suitable way to represent the set of edges. Suppose a simple graph g has 8 vertices.

Let’s assume an undirected graph with vertices. Is there a simple way to calculate this if not, are there some values of n for which this is easier to find out? Let's choose a second node n2:

What is the maximum size (edge count) of a directed acyclic graph? We need to find the maximum number of edges in a graph with two connected components. What is the maximum number of edges a planar subgraph of $k_n$ can have?