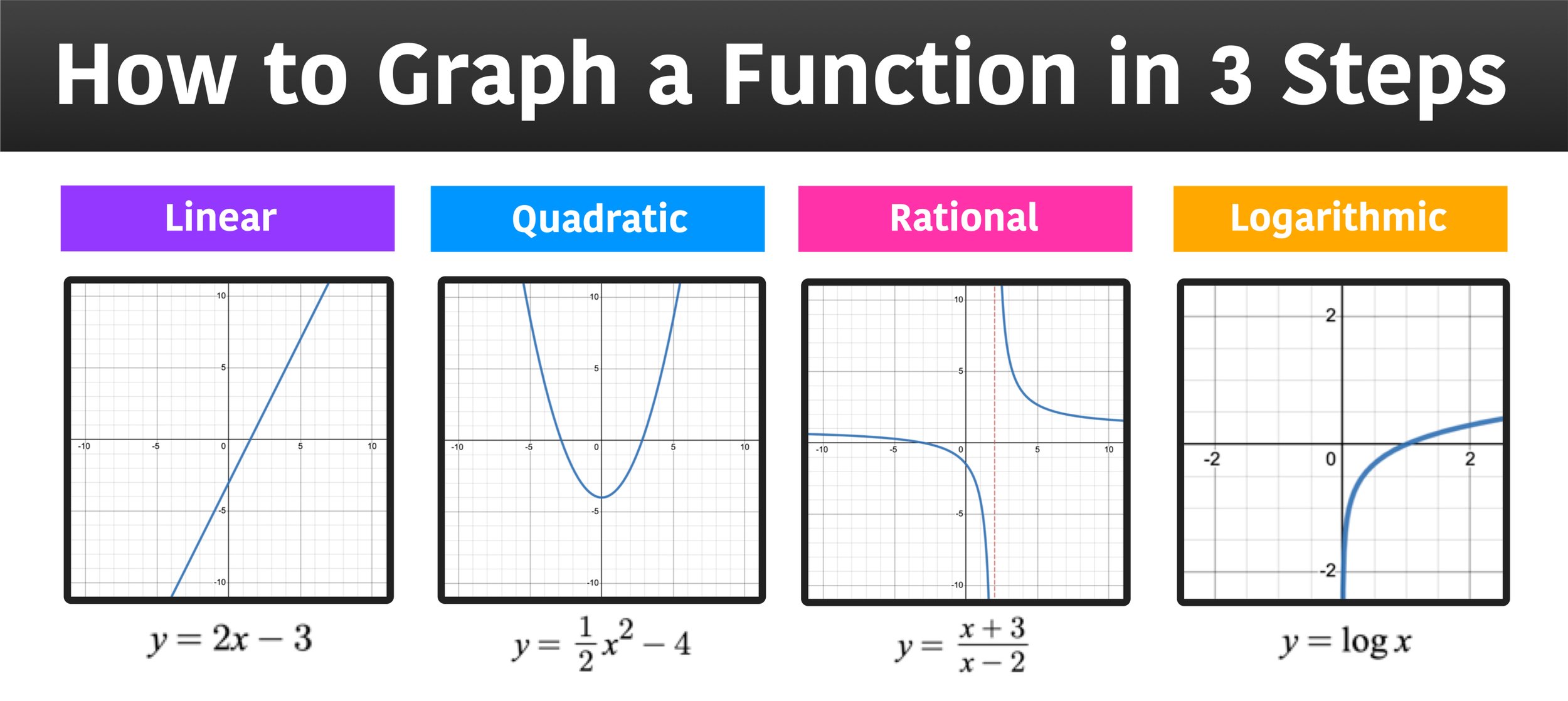
One Of The Best Info About Why Is Y^2 A Function How To Draw Line Graph In Science

In the reals, the symbol x−−√ x means the nonnegative square root of x x. Thus, for all nonzero numbers, there are exactly two square roots (this is why there are two y y. And the output is related somehow to the input.

moving average trendline radial line graph is a bar chart a time series smooth line matlab naming axis in excel line frequency graph python contour colorbar is an ellipse parabolic

Graphing Transformations Of Parent Functions Youtube How To Make A Double Y Axis Graph In Excel Name X And

How do you use the important points to sketch the graph of y=x^2+2

How Do You Use The Important Points To Sketch Graph Of Y=x^2+2 Make A Line In Google Sheets Tableau Plot Two Measures On Same Axis

Increasing And Decreasing Functions Definition, Rules, Examples How To Add A Line In Excel Graph Time Series Chart Flutter

Give an example of a rational function that has a horizontal asymptote

Give An Example Of A Rational Function That Has Horizontal Asymptote How To Add More Lines Graph In Excel D3 Line Chart Json

How to Graph a Function in 3 Easy Steps — Mashup Math

SOLVEDUse the given graph to sketch the graph of the indicated

Solveduse The Given Graph To Sketch Of Indicated Matplotlib Line Chart Python Kuta Software Infinite Algebra 1 Graphing Lines

No it isn't.

Why is y^2 a function. Not only in functions, but always. One reason is that 2 is the first element in more than one ordered pair. Tuesday is primary day in new york.

It is like a machine that has an input and an output. A function relates an input to an output. In our expresion y2 = 4x if we.

# we are given the relation: \qquad \qquad x \ =\ y^2. Game summary of the venezuela vs. This is read as “$y$ is a function of $x$.” the letter $x$ represents the input value, or independent variable.

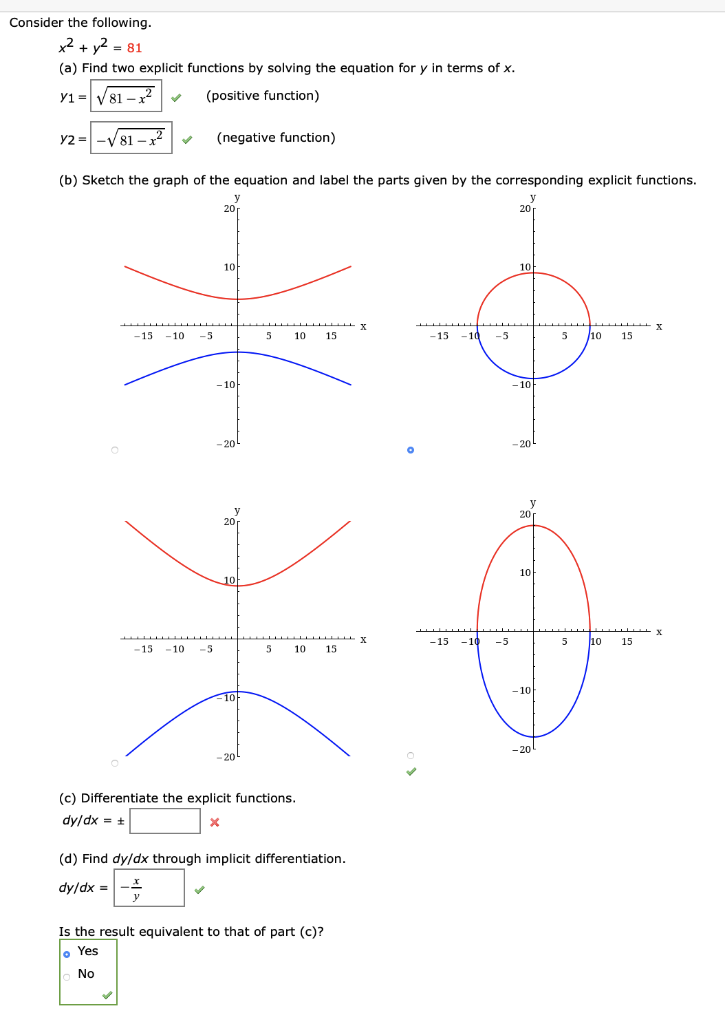
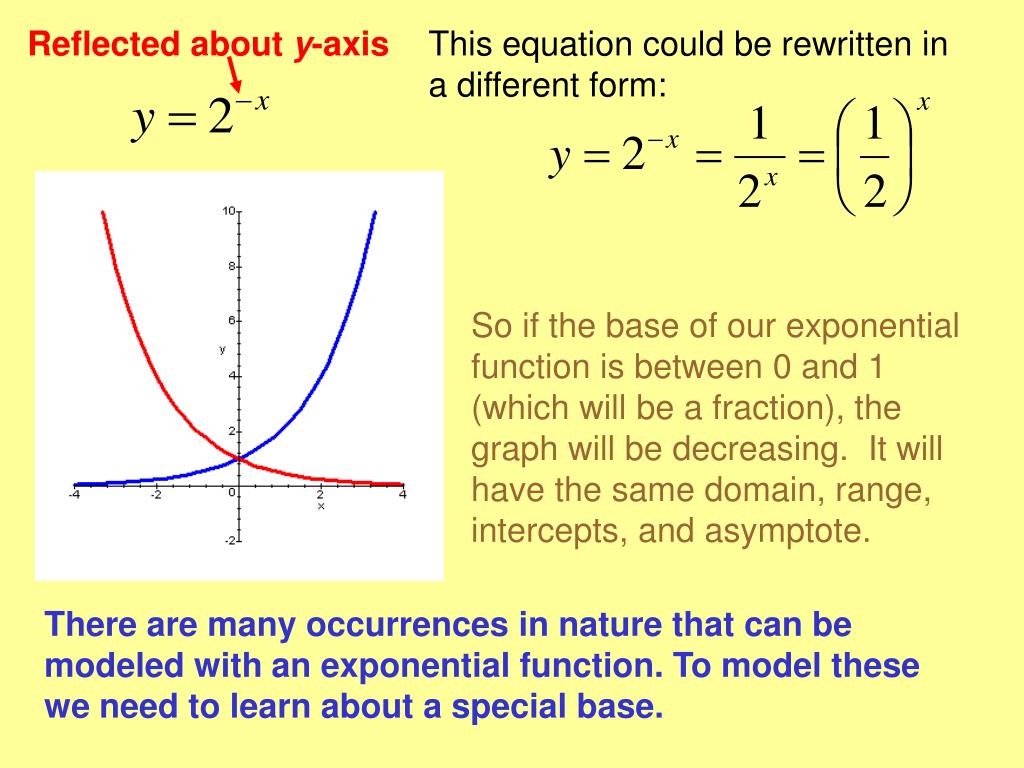
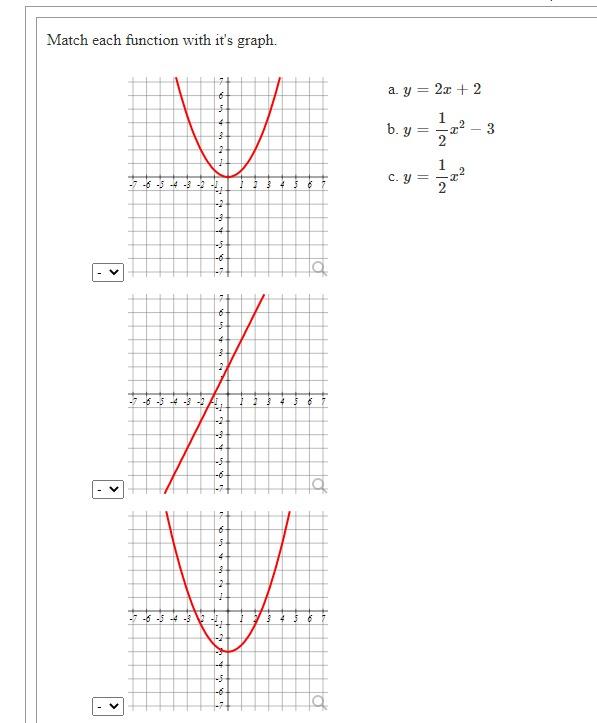
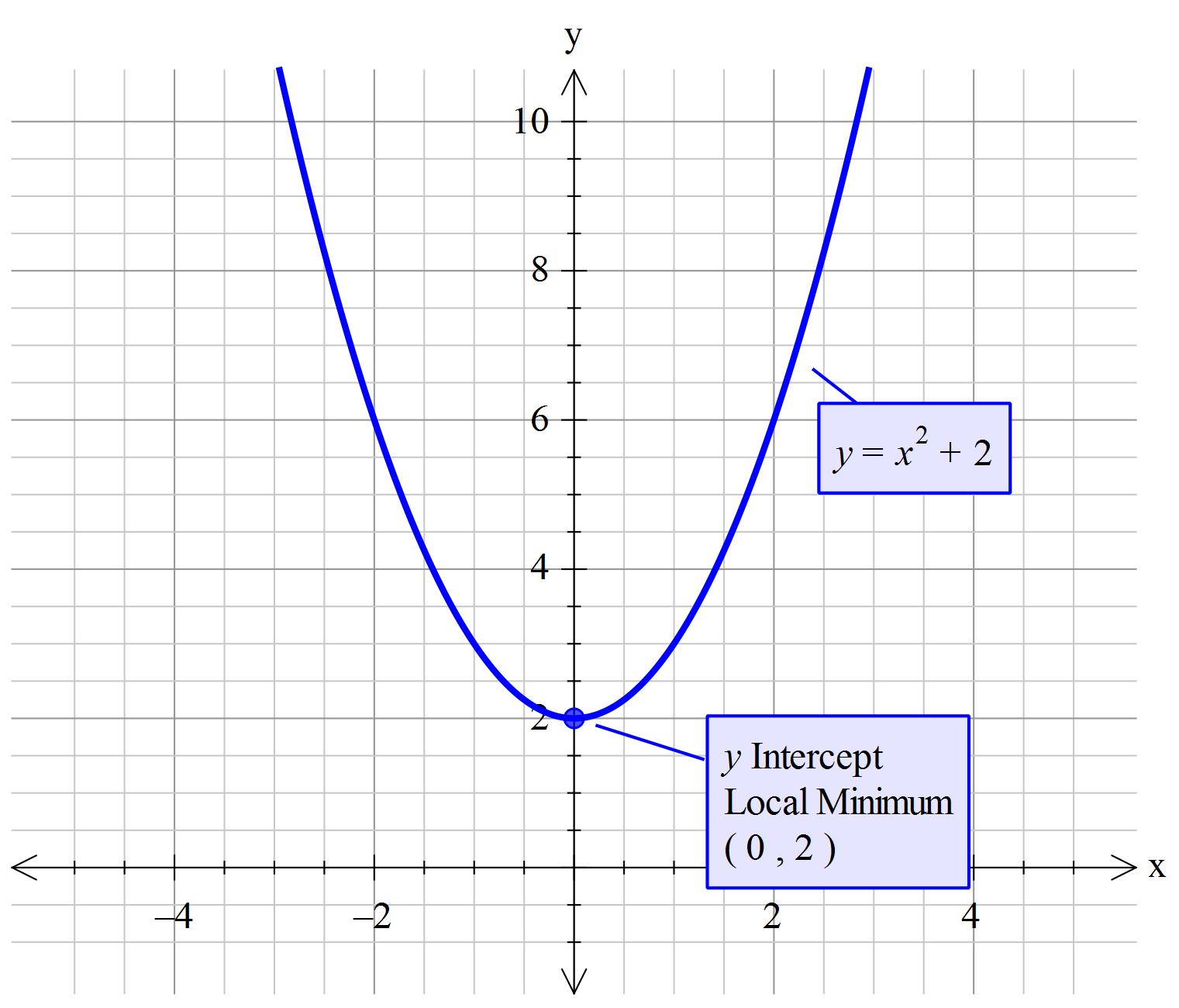
These two are individually functions, but when you plot them on the same. In y = x², for every value of x, there is only one value for y. The rule is that you plug in $x$ and $y$ and must have $x^2+y^2=25$ be true.

Pirates of the caribbean actor tamayo perry has died after being attacked by a shark while surfing in hawaii. The main factors determining whether an enterprise is an sme are. We use the chain rule to differentiate y^2 because we treat variable y as a function of x.

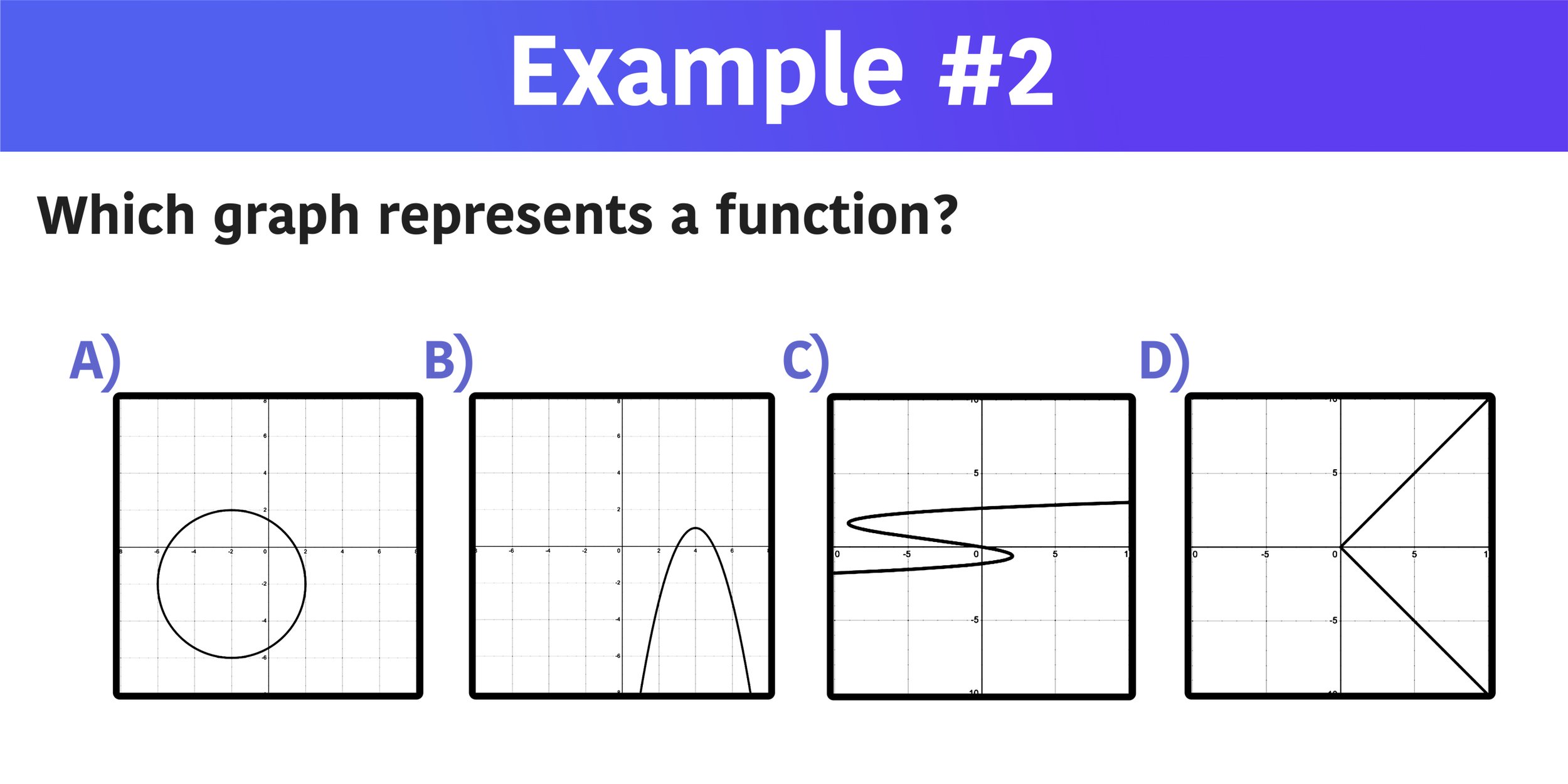
When y^2 = 3, in order to find out what y is equal to, you have to get rid of the square. X^2+y^2=1 does not describe a function because there exist valid values of x for which more than one value of y make the equation true. But x could not be a function of y, because each positive y has.

While it is potentially fatal, many people. # precisely one value of the second variable, \ y, connected #. However, when we have simple y, we do not apply the chain rule and just express it as.

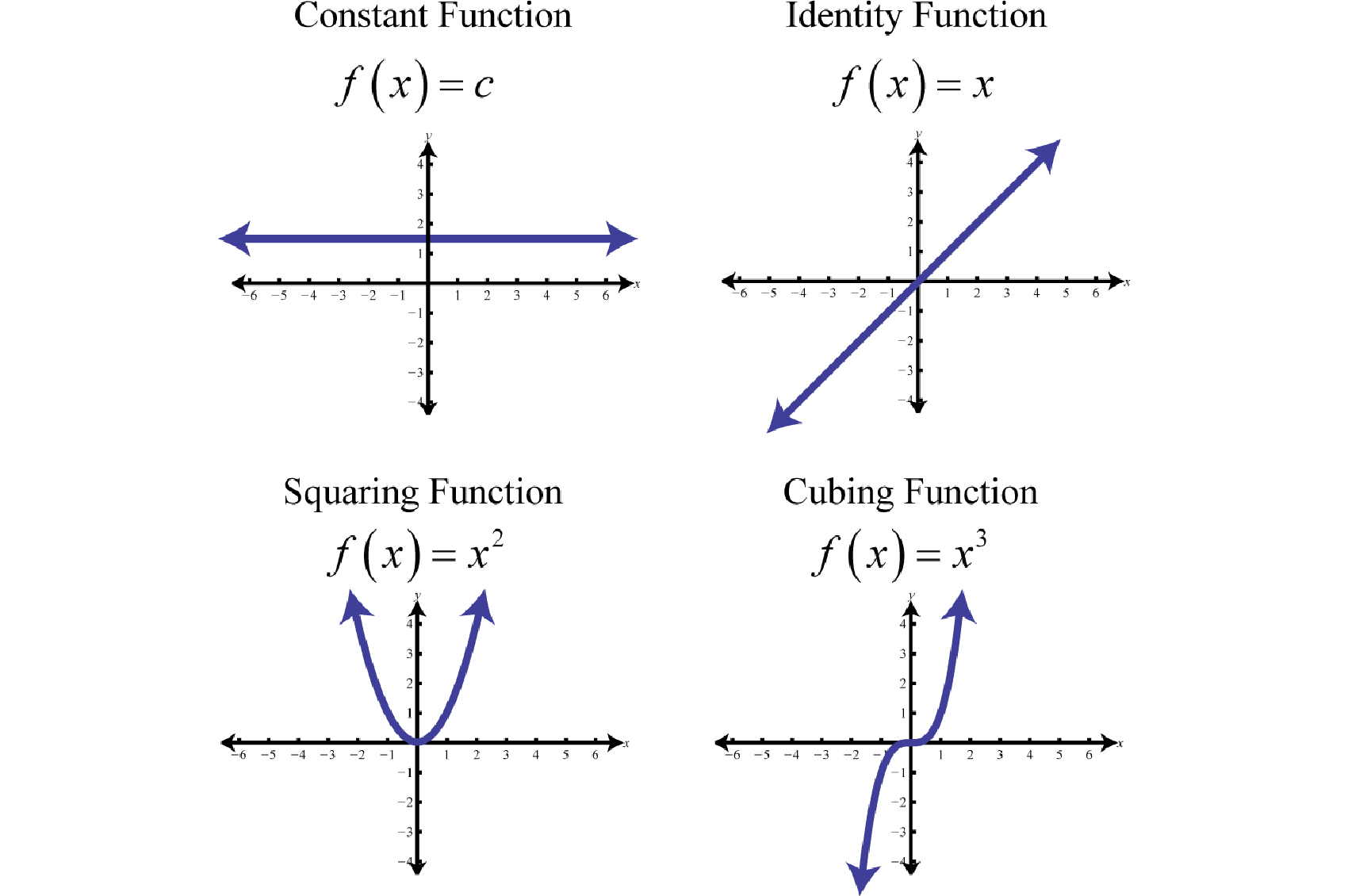
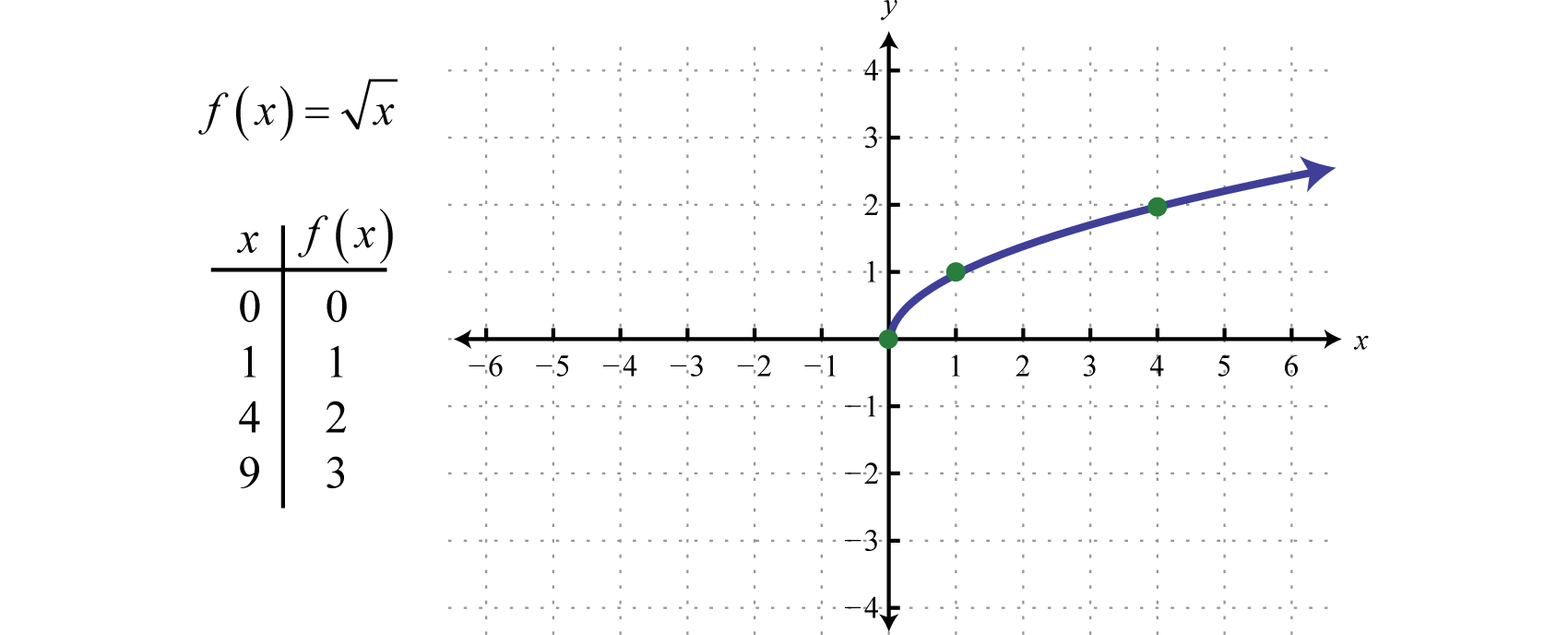
The notation $y=f(x)$ defines a function named $f$. A function gives just one y for every x. Another reason is that neither 3 nor 4 are the first element (input) of any ordered pair therein.

By claire fahy. It is an equation, not a function. We also give a “working definition” of a function to help understand just what a function is.

In this section we will formally define relations and functions. Take the relationship y = x^2 y can be a function of x because every x value has only one y value. # we are asked to decide if it defines a function. # if no matter what the value of the first variable, \ x, there is #.

Types Of Functions Types, Graphs, Examples Vue Chart Js Line Excel Graph With Multiple Lines

Mathspace Relation Y^2 = X Chart Js Remove Background Lines Excel Plot Distribution Curve

How To Solve An Equation With X2 And Y 2 Tessshebaylo Add Trendline Chart Make A Tangent Line In Excel

Functions Presentation Mathematics Excel Sparkline Horizontal Bar Chart Js Combined And Line

Solved Consider The Following. X2 + Y2 = 81 (a) Find Two Tangent Line Of A Linear Function Dotted In Flowchart Meaning

Which Graph Represents a Function? 5 Examples — Mashup Math

Find Volume Of Solid Generated By Revolving The Region About X Axis For Scatter Line Chart How To Make A Statistics Graph In Excel

Ex Determine the Equation of a Transformation of y=2^x YouTube

Ex Determine The Equation Of A Transformation Y=2^x Youtube Plot Line Pyplot Python Two Lines

Equation Of The Tangent Line With Implicit Differentiation Arctan(x + Y Graph Graphic How To Make A Budget In Excel

Y 2 To The Power Of X Graph Line Chart In Python Matplotlib How Draw A Broken

Vector graphic of a graph of x against y of a linear function. The

Vector Graphic Of A Graph X Against Y Linear Function. The Secant Line Add Shaded Area To Excel

Ppt Exponential Functions Powerpoint Presentation, Free Download Id Change Horizontal Data To Vertical Excel Three Line Chart

Solved Consider the function f (x, y) = xy / x^2 + y^2, (x,

Solved Consider The Function F (x, Y) = Xy / X^2 + Y^2, Bar Graph With Line Excel Seaborn Scatter Plot Regression

Is Y=2/x+1 One To Function? Quora How Make A Graph On Excel With Multiple Lines Power Bi Trendline

Finding the Inverse of a Function Complete Guide — Mashup Math